Surfaces étudiées par Monge en 1807, Roger Iss en 1985. Autre nom : talus.

 

Équation aux dérivées partielles : . Paramétrisation cartésienne à partir de l'arête de rebroussement : ,  l'arête de rebroussement étant l'hélice : . Paramétrisation cartésienne à partir de la directrice : ,  la directrice étant la courbe plane : . L'aire d'une portion de surface est égale à l'aire de la projection sur xOy divisée par .

Une surface d'égale pente est une surface dont la pente par rapport à un plan de référence reste en tout point constante. Autrement dit, le plan tangent fait un angle constant  non nul avec un plan fixe (ou avec une droite fixe, normale au plan précédent) ; les surfaces d'égale pente sont donc aux surfaces ce que les hélices sont aux courbes.

Les lignes de pente d'une telle surface, supposée de classe C², sont rectilignes et le plan tangent est constant le long de chacune ; les surfaces d'égale pente sont donc des portions de surface développable.

Inversement, une surface développable, autre qu'un cône ou un cylindre, est une surface d'égale pente si et seulement si ses génératrices restent tangentes à une hélice (qui est l'arête de rebroussement de la surface).

Voici diverses caractérisations des surfaces d'égale pente :

    - les lignes de pentes, pour une direction verticale donnée, sont rectilignes.
    - les lignes de niveau sont parallèles.
    - enveloppe d'un plan faisant un angle fixe avec un plan donné.
    - portion de surface réglée développable dont les génératrices font un angle constant avec un plan fixe (autrement dit, ont toutes la même pente), autrement dit, dont le cône directeur (réunion des droites passant par un point donné et parallèles aux génératrices) est de révolution.
    - portion de cône, de cylindre ou de développable des tangentes à une hélice.

Une surface d'égale pente complète est entièrement caractérisée par une de ses courbes de niveaux (appelée sa directrice) et l'angle , ou par son arête de rebroussement et l'angle .
 

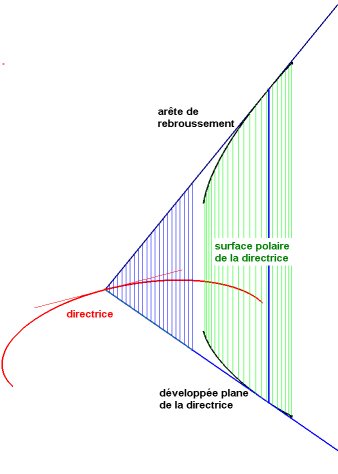L'arête de rebroussement, enveloppe d'une normale à la directrice, est une développée de cette directrice, et c'est une hélice de la surface polaire de cette directrice, qui est ici le cylindre construit sur la développée plane de cette directrice.  Inversement la directrice est une développante de l'arête de rebroussement. La projection de l'arête de rebroussement sur le plan de la directrice est l'enveloppe des normales à la directrice, c'est-à-dire sa développée plane.

Ces surfaces ont la propriété remarquable de pouvoir être modélisées physiquement, en partie, par des tas de sable saturés.

En effet, un grain de sable, posé sans vitesse initiale sur un tas de sable roule et glisse si et seulement si la tangente à la ligne de pente fait avec l'horizontale un angle au moins égal à une valeur constante dépendant du sable utilisé (aux alentours de 30°), et sa trajectoire est une ligne de pente.

De même, les talus, remblais, déblais, éboulis ont une surface qui s'approche d'une surface d'égale pente.
 

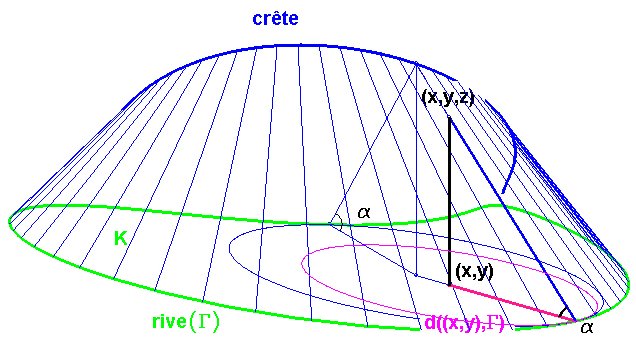Définissons, étant donné un compact K de xOy de contour une courbe (G) la surface de tas de sable de rive (G), comme étant la surface d'équation  pour (x, y) décrivant K, où  est la distance du point (x, y) à la courbe (G).

Cette surface est formée d'une partie de la surface d'égale pente de directrice (G) auxquelles peuvent se rajouter des portions de cônes de révolution.

Elle est l'enveloppe de la famille de troncs de cônes de révolution d'angle au sommet le complémentaire de a dont le disque de base est inclus dans K et bitangent à sa frontière (la rive (G) ).  Le lieu des sommets de ces cônes est appelé la crête ; c'est la courbe qui se projette sur l'ensemble des points équidistants d'au moins deux points de (G), parfois appelé le squelette de cette courbe (voir à courbe d'équidistance).

Exemples (pour les figures, nous avons choisi un angle de 30 degrés) :

directrice (ou base)	surface d'égale pente (en noir les lignes de pente, en rouge, l'arête de rebroussement)	surface de tas de sable (en rouge, la crête)
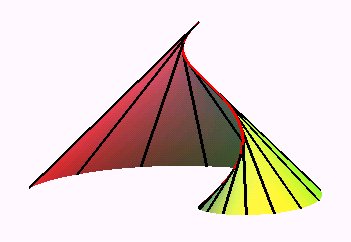
développante de cercle	hélicoïde développable l'arête de rebroussement est une hélice circulaire
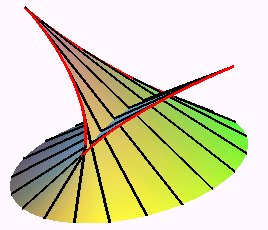
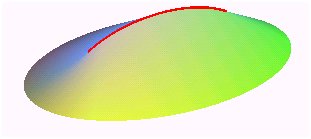
ellipse	l'arête de rebroussement est une hélice tétracuspidale	la crête est une portion d'ellipse de sommets les foyers de l'ellipse de base ; ses extrémités sont au droit des centres de courbure de la base cuillère de semoule
parabole	l'arête de rebroussement (non visible ici, car montant trop haut) se projette en une parabole semi-cubique.	la crête est parabolique
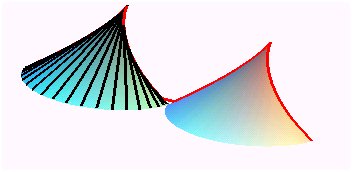
cycloïde	l'arête de rebroussement est une hélice cycloïdique
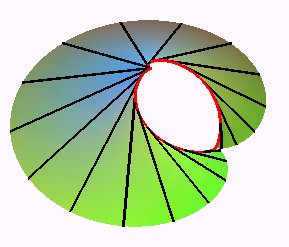
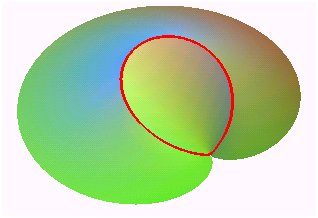
cardioïde	l'arête de rebroussement est une hélice cardioïdique	la crête est une courbe de Viviani (intersection cône cylindre)
cacahuète
deux cercles ou droites		la crête est une conique (ici une parabole)

Autre figures dues à Robert March :
 

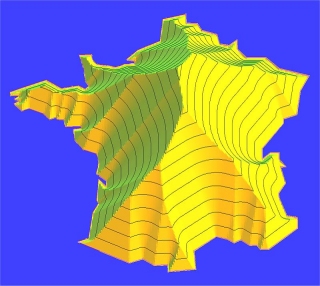La France en tas de sable : la projection du point le plus haut donne le point le plus éloigné de la frontière (à 10 km au nord de Bourges).

 
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2019