Julia set, Juliasche Menge
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
Julia set, Juliasche Menge
| Notion étudiée par Julia en 1918.
Gaston Julia (1893 - 1979) : mathématicien français. Sites : fr.wikipedia.org/wiki/Ensemble_de_Julia mieux, le site en anglais : en.wikipedia.org/wiki/Julia_set maths.wikidot.com/mandelbrot-et-julia josephv.test.free.fr/fractal/mandelbrot/JULIA-MANDELBROT.html nylander.wordpress.com/category/fractals/ Excellent logiciel de tracé dû à Arnaud Chéritat utilisé pour les figures grises ci-dessous : www.math.univ-toulouse.fr/~cheritat/documents/DH_Drawer.zip |
À toute fonction f entière
du plan complexe dans lui-même et tout point de départ 
est associée la suite 
des itérés successifs de
par f.
Le plan est alors partagé entre l'ensemble des
point
pour lesquels la suite 
est bornée (les prisonniers de f), et les autres (les fugitifs).
L'ensemble de Julia 
associé à f est alors la frontière commune
de ces deux ensembles ; c'est, autrement dit, la ligne de démarcation
entre les prisonniers et les fugitifs. Ses éléments sont
les points tels qu'une infime variation fait complètement changer
le comportement de la suite .
Le complémentaire de
est appelé l'ensemble
de Fatou de f.
L'ensemble des prisonniers est appelé l'ensemble
de Julia rempli, noté 
.
Les ensembles de Julia classiques sont ceux associés
aux fonctions 
définies par 
.
Notons que dans ce cas, lorsque la suite est non bornée, elle tend
vers l'infini.
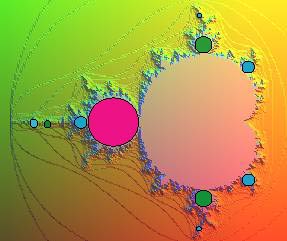
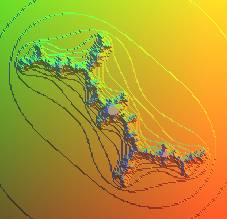
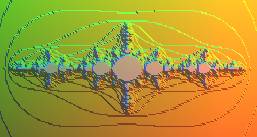
On montre que, dans ce dernier cas, si la suite 
dépasse 2 en module, alors elle tend vers l'infini ; on en déduit
que  est
l'intersection des domaines Dn (limités
par une courbe algébrique de degré 2n+1
) définis par 
;  est
donc fermé et borné.
La figure de gauche montre, dans le cas c = -1, le tracé des courbes implicites 
pour n = 0,1,2,3 ; malheureusement, à partir de n =
4, la courbe devient illisible.
La figure de droite, qui fait apparaître les 100 premiers domaines ci-dessus, a été obtenue comme suit : appelant "durée de vie" le premier entier n tel que 
dépasse 2, on représente la vue de dessus de la surface associée
à la fonction qui à 
associe 1 si la durée de vie est paire, 0 sinon. |
 |
 |
||
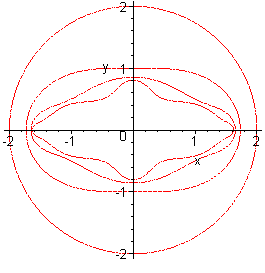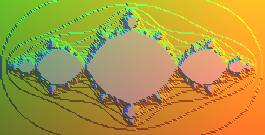
| On obtient une meilleure vision de l'ensemble de Julia
rempli en représentant la fonction qui à
associe sa durée de vie si celle-ci est inférieure à
100, et 100 sinon ; on obtient une surface que l'on pourrait désigner
par "plateau de Julia"; ce plateau, représentant D100
et
les contreforts qui y mènent, donne une bonne idée de l'ensemble
de Julia rempli limite.
A droite on a représenté D100 seul. La partie grise donne une bonne idée de l'ensemble de Julia rempli, et sa frontière de celle de l'ensemble de Julia proprement dit. Programme maple correspondant :
|
 |
 |
||
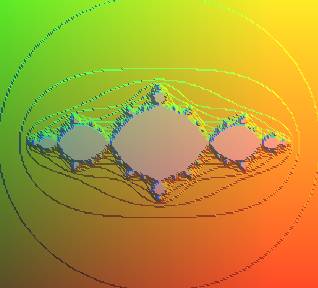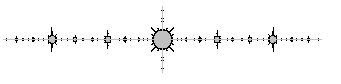
| Une autre méthode très simple donnant rapidement une
idée de l'ensemble de Julia est la méthode dite d'itération
inverse. On montre en effet que l'ensemble de Julia est l'attracteur
du système formé par les deux fonctions réciproques
de ; ce
qui signifie que si un est un des 2n antécédents
n-ième
de 0 (par exemple) par
, la distance de un à l'ensemble de Julia
tend vers 0 ; en pratique on choisit au hasard pour un
l'un des deux antécédents de un-1
.
L'affichage des 1000 premières valeurs de un donne une bonne idée de l'ensemble de Julia (en rouge ci-contre) ; programme Maple correspondant :
|
 |
 |
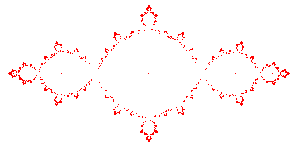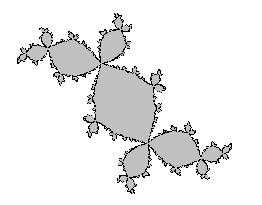
On montre que l'ensemble de Julia 
est connexe ss'il contient 0, ce qui signifie que c est dans l'ensemble
de Mandelbrot.
Des cas de connexité remarquables sont donc ceux où la suite
partant de 0 est périodique, ce qui s'obtient en résolvant  .
Les points c correspondants sont les "centres" des composantes hyperboliques
de l'ensemble de Mandelbrot. |
 |
 |
 
partant de 0 est constante.
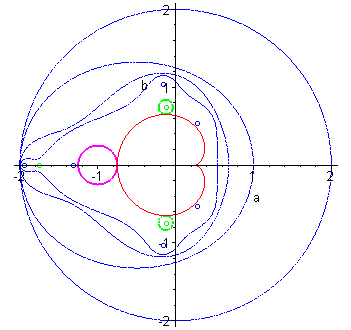L'ensemble de Julia est le cercle de centre 0 et de rayon 1. |
Cas c = -1 (centre de la composante rose ci-dessus) ; la suite
partant de 0 est 2-périodique. Surnom : la basilique. |
  Cas c = -1,7548... (solution réelle de c3+2c²+c+1=0)
; la suite |
partant de 0 est 3-périodique.
L'ensemble de Julia correspondant est dénommé "lapin de Douady". |
 
 
partant de 0 est 4-périodique. |
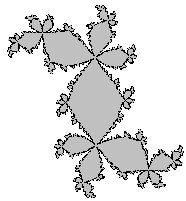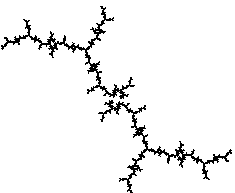 Cas c= -1,310..(solution réelle de 1+2c²+3c3+3c^4+3c^5+c^6=0)
;
|
L'intérieur de l'ensemble de Julia rempli est à
la fois non vide et connexe ssi
possède un point fixe attractif ou indifférent, ce qui signifie
que c se trouve dans la composante principale de l'ensemble de Mandelbrot
(en forme de cardioïde) ou dans sa frontière. L'ensemble de
Julia est alors la frontière du bassin d'attraction du point fixe
attractif ou indifférent et c'est une courbe fermée simple
(mais fractale, sauf pour c = 0), passant par l'autre point fixe,
qui est répulsif.
Ci-dessous, quelques exemples où c se trouve
sur la cardioïde, soit 
.
Cas t = 0, c = 1/4 (pointe de la cardioïde)
|
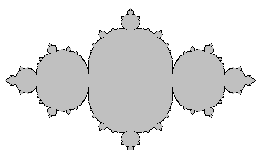
Cas t = pi, c = -3/4 (sommet de la cardioïde)
|
 
Cas t = pi/3 et t = 2pi/3 ; la deuxième valeur correspond exactement au point le plus haut de la cardioïde. |
 Cas t = pi(1 - sqrt(5)) ; l'ensemble de julia rempli est un disque de Siegel. |
Ci-dessous, d'autres cas particuliers d'ensembles de Julia,
où c, point de Misiurewicz,
se trouve sur la frontière de l'ensemble de Mandelbrot ; l'ensemble
de Julia, d'intérieur vide, est alors confondu avec l'ensemble de
Julia rempli.
partant de 0 est constante à partir de z2 ; l'ensemble
de Julia est réduit au segment [-2 , 2 ] ; notons que la première
équipotentielle est une lemniscate
de Bernoulli. |
partant de 0 est 2-périodique à partir de z2 ;
surnom : la dendrite. |
 
partant de 0 est constante à partir de z4 |
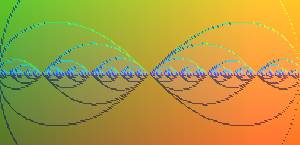
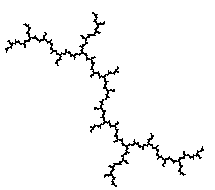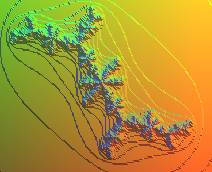Dernier cas : c est en dehors de l'ensemble de
Mandelbrot ; dans ce cas, l'ensemble de Julia est non seulement non connexe,
mais totalement discontinu (ses composantes connexes sont des points).
Cependant, ses points ne sont pas isolés (c'est donc un espace
de Cantor).
Il prend alors le nom de poussière de Fatou.
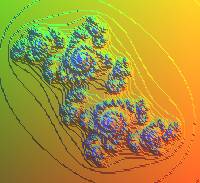 Cas c = -0,63 +0,67 i |
 |
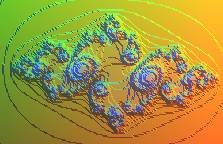
Cas c = -0.76+0.12 i |
 |
 |
 |
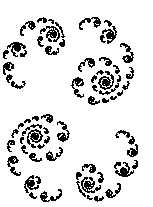| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2011