COURBE DE PEANO
Peano's curve, peanosche Kurve
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE PEANO
Peano's curve, peanosche Kurve
| Courbe étudiée par Peano en 1890.
Giuseppe Peano (1858 - 1932) : mathématicien italien. Voir aussi cet article et aesculier.fr/fichiersMaple/peano/peano.html. |
Paramétrisation cartésienne :
définie,
en posant, en base 3,
|
Définition n°1 :
La courbe de Peano est une courbe remplissant le carré [0, 1]2 définie par l'algorithme :
1) Partager [0, 1]2 en 9 "petits" carrés "égaux" ; numéroter chacun de ces carrés de sorte que deux carrés successifs se touchent par un côté, en commençant par le carré en bas à gauche, et terminant par le carré en haut à gauche ; il y a deux possibilités : nous choisissons le chemin vertical.
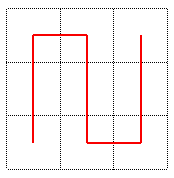
2) Partager chacun de ces carrés en 9 "micro" carrés "égaux" ; numéroter chacun de ces carrés de sorte que deux micro carrés successifs se touchent par un côté, en commençant par le micro-carré en bas à gauche, et terminant par le micro-carré en haut à droite, le premier micro-carré d'un petit carré devant avoir un côté en commun avec le dernier micro-carré du petit carré précédent et le dernier micro-carré devant toucher par un coté le petit carré suivant.
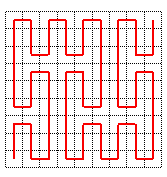
3) Recommencer ce processus à l'infini.
A l'étape n, on obtient donc une suite de
9n carrés 
de côté 
,
deux carrés successifs se touchant par un côté, recouvrant
successivement les carrés 
.
La courbe de Peano approchée du premier type
d'ordre n est alors la ligne brisée joignant les centres successifs
de ces carrés.
 |
 |
|
|
 |
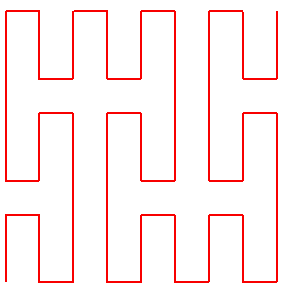
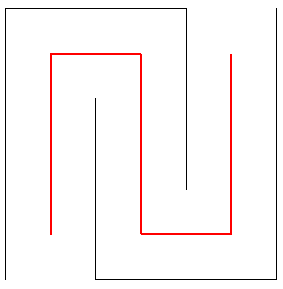
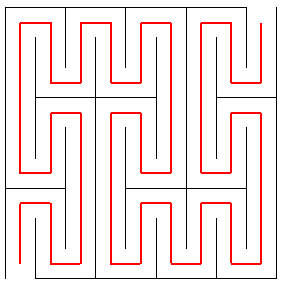
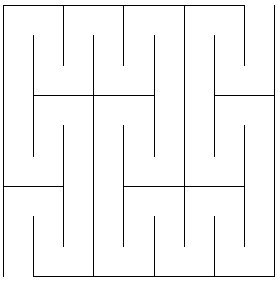
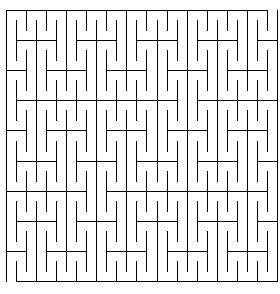
Le labyrinthe de Peano d'ordre n est la
réunion des côtés des carrés
excepté les
côtés joignant deux carrés consécutifs
(et les deux entrées) :
 |
 |
 |
 |
 |
 |
Si t appartient à [0,1[ , posons 
(où [t] désigne la partie entière de t).
Les 
,
pour t fixé, forment une suite de carrés (compacts)
emboîtés dont l’aire tend vers 0 ; leur intersection est donc
réduite à un point 
, point courant de la courbe de Peano.
On démontre que la courbe est continue et que sa trajectoire est dense dans le carré, donc égale à ce carré.
Définition n° 2 :
Etant donné un carré ABCD (ici A(0,0), B(1,0), C(1,1), D(0,1)), la courbe de Peano est la courbe limite de segment de départ [AC] associée à une famille de 9 contractions , similitudes de rapport 1/3, transformant le grand carré en les neuf petits carrés qui le composent, dont le carré plein ABCD est l'attracteur.
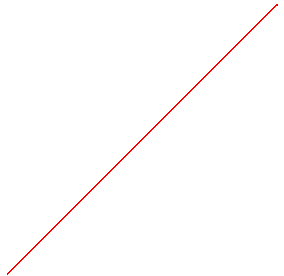
La courbe de Peano approchée du deuxième
type d'ordre n est l'image itérée n-ième
de [AC] par f définie par
.
C'est cette courbe, peu esthétique car on ne comprend pas son tracé
à première vue, qui est en général présentée
comme courbe de Peano.
 |
 |
 |
 |
 |
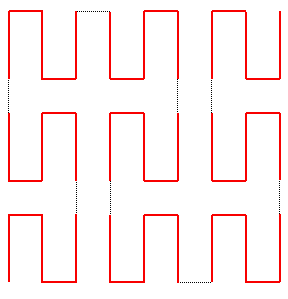
En prenant comme courbe de départ : 
,
on peut retrouver la courbe de Peano du premier type, à condition
de raccorder les morceaux entre eux :
|
|
 |
 |
 |
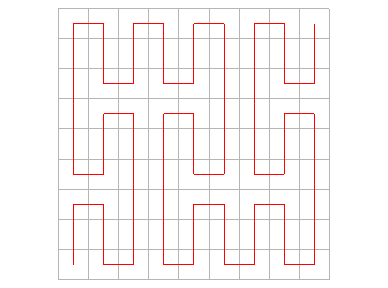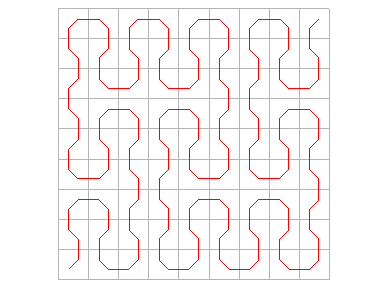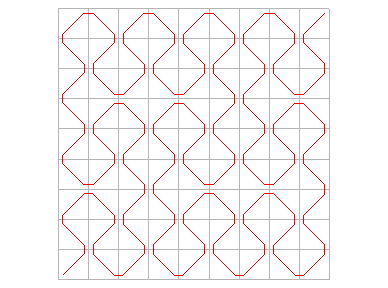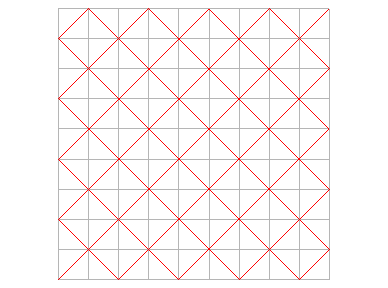
En prenant comme courbe de départ un segment [(a,
a)
, (1–a, 1–a)] et en raccordant, on obtient une suite de courbes
sans point double convergeant aussi vers la courbe de Peano :
 |
 |
 |
 |
Voir des variantes de la courbe de Péano sous le nom de courbes de Wunderlich.
La courbe de Peano étant historiquement le premier
exemple de courbe remplissant un carré, l'expression "courbe de
Péano" désigne aujourd'hui souvent n'importe quelle courbe
remplissante.
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2016
par :
