SINE TORUS
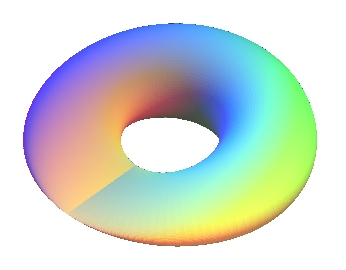
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SINE TORUS
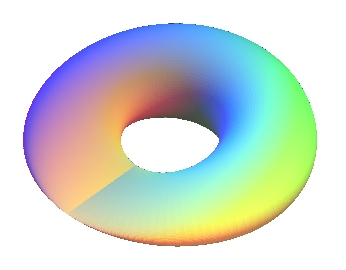
| Homemade name.
The first kind in the case k = 1/2 was studied in 1947 by Maurice El-Milick, surface that he called "one-sided cyclide". See also this article. |
1) First kind:
| Cartesian parametrization: Cylindrical equation for k = 1/2: Corresponding Cartesian equation (algebraic surface of degree 6): a^4 y^2 - 2 a^2 b^2 y^2 + b^4 y^2 - 2 a^2 x^2 y^2 - 2 b^2 x^2 y^2 + x^4 y^2 - 2 a^2 y^4 - 2 b^2 y^4 + 2 x^2 y^4 + y^6 + 4 a^2 x^2 z^2 - 4 b^2 x^2 z^2 - 8 a x^3 z^2 + 4 x^4 z^2 + 4 a^2 y^2 z^2 - 4 b^2 y^2 z^2 - 8 a x y^2 z^2 + 8 x^2 y^2 z^2 + 4 y^4 z^2 + 4 x^2 z^4 + 4 y^2 z^4=0 |
The sine tori of the first kind are the surfaces generated
by the rotation of a variable ellipse around an axis, with the ellipse
located in a plane perpendicular to the axis, and one axis of the ellipse
remaining constant while the other varies sinusoidally.
| We obtain a 3D immersion of the Klein bottle for k = 1/2 and a > b > 0; the principal vertices of the generating ellipse describe two circles and the secondary vertices describe a Viviani curve (in blue opposite). | 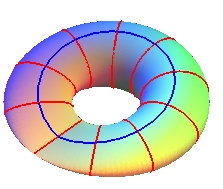 |
| Opposite, the model made in 1947 by Maurice El-Milick, preserved at the Institut Henri Poincaré. | 
Photo: François Apery |
| In the case b = a, still with k = 1/2,
the surface obtained is none other, up to scaling, than the cross-cap.
The removal of the central hole made the genus decrease by 1, and therefore we got from the Klein bottle to the projective plane. |
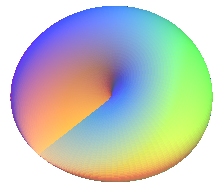 |
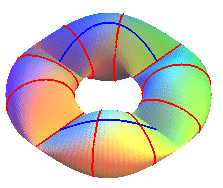
| For any k, the secondary vertices of the ellipse describe one or two cylindrical sine waves with parameter k. | 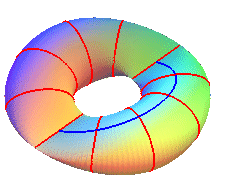
Case k = 1: orientable surface; the blue curve is an ellipse |

Case k = 3/2: one-sided surface, immersion of the Klein bottle |
 |
2) Second kind:
| Cartesian parametrization: |
The sine tori of the second kind are the surfaces generated
by the rotation of a variable circle around an axis, with the circle on
a plane perpendicular to the axis, and the radius of the circle varying
sinusoidally; in other words, it is a tube
the bore of which is a circle with radius that varies sinusoidally.
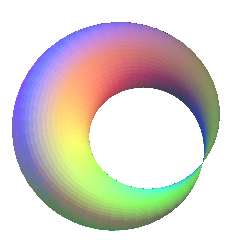
| For k = 1/2, we get the surface with one conical
point called "pinched
torus".
no to be mistaken for the horn Dupin cyclide: 
(for the first one, the projection on xOy is delimited by a limaçon of Pascal with a loop, whereas for the second one, it is delimited by two tangent circles). |
 |
| Some other examples: |

Case k = 1 |

Case k = 2 |

Case k = 3 |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017