Elliptic paraboloid

ELLIPTIC PARABOLOID

Cartesian equation: , p, q >0. Quadric. Cartesian parametrization: . Parametrization the coordinate lines of which are the curvature lines (case ): (figure opposite). Gaussian curvature: .	The projections on xOy of the curvature lines are the ellipses , and the hyperbolas , with the general formula: .
Volume of the paraboloidal bowl with height h, the semi-axes of the ellipse at the summit being a and b (): (half of the circumscribed cylinder).

The elliptic paraboloids can be defined as the surfaces generated by the translation of a parabola (here with parameter p) along a parabola in the same direction (here with parameter q) (they are therefore translation surfaces).

Note that when the two parabolas have opposite directions, we get the hyperbolic paraboloid.

The sections by vertical planes are parabolas and the sections by horizontal planes are ellipses.

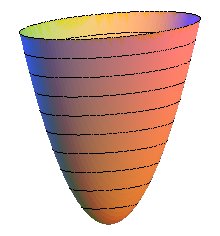
View of one of the two families of circles included in any elliptic paraboloid, even if it is not of revolution, with the corresponding umbilic.

The paraboloid of revolution (or circular paraboloid) corresponds to the case p = q.

See at hyperbolic paraboloid a boxed text about confocal paraboloids.

Bird nest shaped like a paraboloid. If you have something better...

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra