binoid, or catenoid

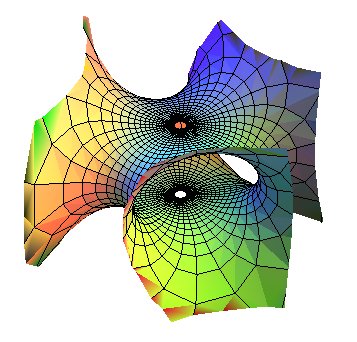
trinoid

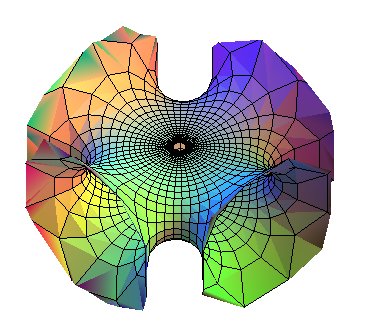
quadrinoid

 

Surface studied by Jorge and Meeks in 1983. The name is based on the prefix tri- and the suffix noid, that comes from catenoid.

 

Parametrization of the trinoid: [-1/9*(-3*exp(2*u)-3*exp(u)*cos(v)-3*exp(3*u)*cos(v)+8*ln(-2*exp(u)*cos(v)+1+exp(2*u))*exp(2*u)*cos(v)^2+4*ln(-2*exp(u)*cos(v)+1+exp(2*u))*exp(u)*cos(v)-4*ln(4*exp(2*u)*cos(v)^2+exp(4*u)+2*exp(3*u)*cos(v)-exp(2*u)+2*exp(u)*cos(v)+1)*exp(2*u)*cos(v)^2+2*ln(-2*exp(u)*cos(v)+1+exp(2*u))-ln(4*exp(2*u)*cos(v)^2+exp(4*u)+2*exp(3*u)*cos(v)-exp(2*u)+2*exp(u)*cos(v)+1)-2*ln(4*exp(2*u)*cos(v)^2+exp(4*u)+2*exp(3*u)*cos(v)-exp(2*u)+2*exp(u)*cos(v)+1)*exp(u)*cos(v)+4*ln(-2*exp(u)*cos(v)+1+exp(2*u))*exp(3*u)*cos(v)-2*ln(4*exp(2*u)*cos(v)^2+exp(4*u)+2*exp(3*u)*cos(v)-exp(2*u)+2*exp(u)*cos(v)+1)*exp(3*u)*cos(v)-2*ln(-2*exp(u)*cos(v)+1+exp(2*u))*exp(2*u)+2*ln(-2*exp(u)*cos(v)+1+exp(2*u))*exp(4*u)+ln(4*exp(2*u)*cos(v)^2+exp(4*u)+2*exp(3*u)*cos(v)-exp(2*u)+2*exp(u)*cos(v)+1)*exp(2*u)-ln(4*exp(2*u)*cos(v)^2+exp(4*u)+2*exp(3*u)*cos(v)-exp(2*u)+2*exp(u)*cos(v)+1)*exp(4*u))/(4*exp(2*u)*cos(v)^2+exp(4*u)+2*exp(3*u)*cos(v)-exp(2*u)+2*exp(u)*cos(v)+1),   1/9*(3^(1/2)*ln((3^(1/2)*exp(u)*sin(v)+exp(u)*cos(v)+1+exp(2*u))/(exp(u)*cos(v)+1+exp(2*u)-3^(1/2)*exp(u)*sin(v)))+6*exp(2*u)*cos(v)*sin(v)+3*exp(u)*sin(v)-8*3^(1/2)*ln((3^(1/2)*exp(u)*sin(v)+exp(u)*cos(v)+1+exp(2*u))/(exp(u)*cos(v)+1+exp(2*u)-3^(1/2)*exp(u)*sin(v)))*exp(3*u)*cos(v)^3+3*exp(5*u)*sin(v)+3^(1/2)*ln((3^(1/2)*exp(u)*sin(v)+exp(u)*cos(v)+1+exp(2*u))/(exp(u)*cos(v)+1+exp(2*u)-3^(1/2)*exp(u)*sin(v)))*exp(6*u)+6*3^(1/2)*ln((3^(1/2)*exp(u)*sin(v)+exp(u)*cos(v)+1+exp(2*u))/(exp(u)*cos(v)+1+exp(2*u)-3^(1/2)*exp(u)*sin(v)))*exp(3*u)*cos(v)+6*exp(4*u)*cos(v)*sin(v))/(1+exp(6*u)+6*exp(3*u)*cos(v)-8*exp(3*u)*cos(v)^3),   2/3*exp(3*u)*(4*cos(v)^3-3*cos(v)-exp(3*u))/(1+exp(6*u)+6*exp(3*u)*cos(v)-8*exp(3*u)*cos(v)^3)]

The trinoid, and more generally, the n-noids are minimal surfaces with rotational symmetry of order n and n infinite sheets of the kind of those of the catenoid (and what could be called binoid is in fact none other than the catenoid).
They are obtained by taking  (and then ) in the Weierstrass parametrization of a minimal surface: .

Series of n = 2,3,4,5-noids, with petal-like boundaries, by Alain Esculier.

These surfaces can be generalized into the surfaces with constant mean curvature (not necessarily equal to zero) having an order n symmetry, see for example here.
 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017