OVALE DE CAYLEY
Cayley
oval, cayleysches Oval
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
OVALE DE CAYLEY
Cayley
oval, cayleysches Oval

| Courbe étudiée par Cayley en 1857.
Arthur Cayley (1821-1895) : mathématicien anglais. |
| Équation bifocale : Équation cartésienne : Paramétrisation cartésienne : |
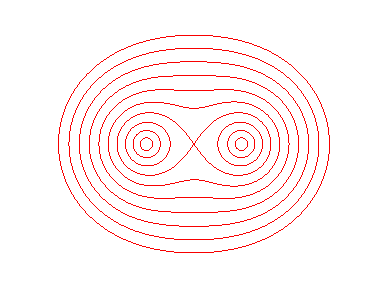
Les ovales de Cayley sont les lieux des points du plan dont la moyenne harmonique des distances à 2 points, les foyers, est constante (= b).
Ce sont donc les lignes équipotentielles du potentiel électrostatique créé par deux charges égales placées aux foyers (ou du potentiel gravitationnel créé par deux masses identiques).
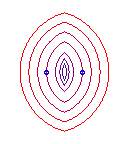
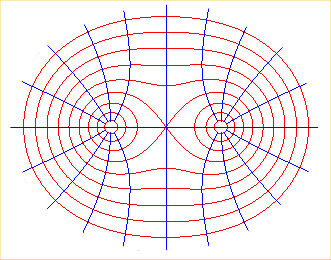 vue des équipotentielles, en rouge, avec les lignes de champ.
vue des équipotentielles, en rouge, avec les lignes de champ.
Cas b < a : l'"ovale" est formé
de 2 courbes en forme d'oeuf symétriques par rapport à O.
Cas e = 1 (b = a) la courbe
a une forme de 8.
Cas :
l’ovale a alors la forme d’une "ellipse" déprimée aux deux
sommets du petit axe.
Cas
: l’ovale a enfin la forme ovale, tendant vers une forme circulaire quand
e
augmente.
Tout ceci rappelle fortement les ovales
de Cassini (qui sont, eux, des quartiques) ; on peut en effet placer
ces deux familles dans le cas plus général des lieux des
points du plan dont la moyenne d'ordre p des distances à
2 points est constante, d'équation bifocale
; on voit ci-dessous que les ovales de Cassini et de Cayley sont assez
proches ; on peut les différencier par les tangentes en O.
|
|
|
|
|
|
|
|
|
|
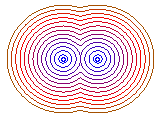
b = 0 : foyers, b = a : deux cercles tangents |
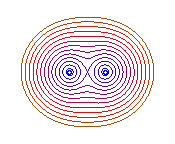
b = 0 : 2 points, b = a : huit |
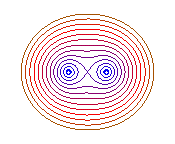
b = 0 : 2 points, b = a : huit |
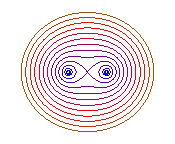
b = 0 : 2 points, b = a : huit |
|
|
|
|
|
|
|
|
|
|
|
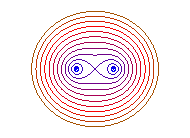
b = 0 : 2 points, b = a : huit |
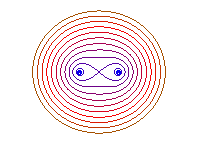
b = 0 : 2 points, b = a : huit |
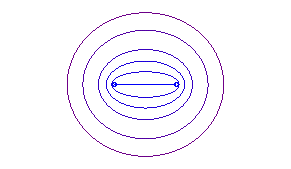
b = a : segment |
|
|
|
|
|
|
|
|
|
|
|
|
|
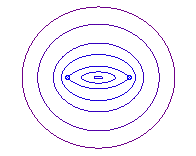
b = a : point O. |
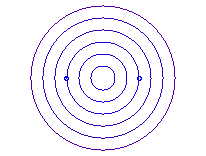
b = a : point O. |
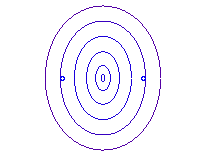
b = a : point O. |
b = a : point O |
|
|
|
Une autre généralisation consiste à
placer des charges quelconques en des points quelconques ; les lignes équipotentielles,
d'équation multifocale
s'appellent les équipotentielles de Cayley : elles sont aux
ovales de Cayley ce que sont les cassiniennes
aux ovales de Cassini.
Voici par exemple les équipotentielles (en rouge),
d'équation
et les lignes de champ correspondantes (en bleu) dans le cas de deux charges
opposées.
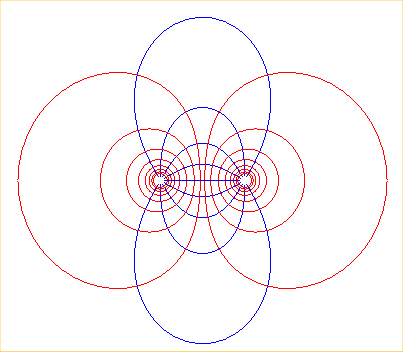
Pour le cas limite de ces dernières courbes quand les pôles se rapprochent, voir à courbe du dipôle.
On peut bien sur généraliser ceci aux courbes
d'équation multifocale
qui redonnent les équipotentielles de Cayley pour p = – 1.
Pour p = – 2, on obtient les courbes dites "isophoniques". Ce sont
les courbes joignant les points où l'intensité sonore (ou
lumineuse) dues à des souces sonores (ou lumineuses) placées
aux foyers est identiques ; voici par exemple des courbes isophoniques
pour des sources identiques placées aux sommets d'un triangle :
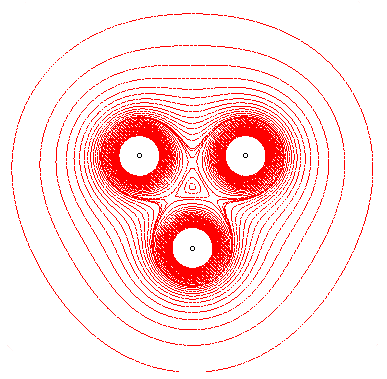
Pour d'autres courbes définie par des phénomènes
sonores, voir les courbes de Loriga.
Pour d'autres équipotentielles et lignes de champ, voir cette page.

Le hibou de Cayley....
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2023