OVALE DE CASSINI
Cassinian
oval, Cassinisches Oval
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
OVALE DE CASSINI
Cassinian
oval, Cassinisches Oval

| Courbe étudiée par Cassini en 1680 et Malfatti
en 1781.
Nom famillier : les yeux de chat. Jean-Dominique Cassini (1625-1712) : astronome français.
|
| Équation bifocale : Paramétrisation cartésienne : avec Équation polaire : l'équation avec " – " ne donnant des points réels que lorsque e Équation cartésienne : soit encore : Quartique bicirculaire elliptique (rationnelle pour e = 1).
Aire d'un ovale pour e < 1 : |
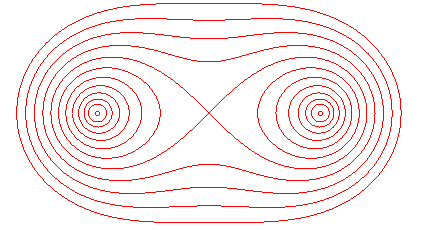
Les ovales de Cassini sont les lieux des points du plan dont la moyenne géométrique des distances à 2 points, les foyers, est constante (égale à b).
Ce sont donc aussi les lignes
de champ du champ vectoriel ,
somme de deux champs orthoradiaux en 1/r.
Dans le cas e < 1 (b < a) : l'"ovale" est formé de 2 courbes en forme d'oeufs symétriques par rapport à O, d’équations tripolaires :
La courbe est dans ce cas anallagmatique
: conservation par l'inversion de centre O et de puissance
; on a donc une génération cyclique
: la déférente est l'hyperbole
avec
et
,
et le cercle directeur (de rayon Öp)
en est le cercle de Monge.
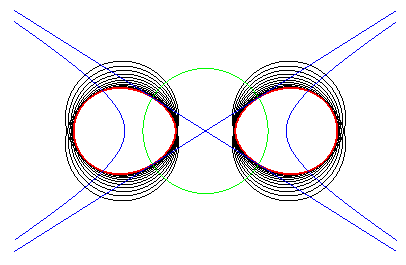
L' ovale de Cassini comme enveloppe des cercles centrés sur une hyperbole et orthogonaux à son cercle de Monge.
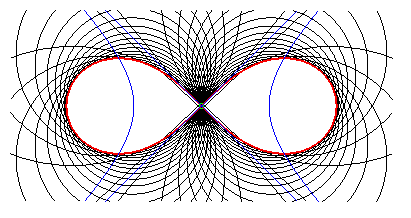
Dans ce cas, l'hyperbole est équilatère et le cercle
vert est réduit à O.
Dans le cas e > 1, l'ovale de Cassini réel n'est plus anallagmatique, mais la courbe complexe l'est encore, avec une puissance d'inversion complexe.
Pour
(
), l’ovale
a alors la forme d’une "ellipse" déprimée aux deux sommets
du petit axe.
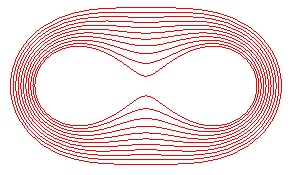
Pour ,
l’ovale a enfin la forme ovale. Valéry
Ochkov propose de le baptiser "ovale de Tolstoï" pour sa ressemblance
avec l'hippodrome de Tsarskoïe Selo près de Saint Pétersbourg,
hippodrome dont il est fait mention dans le roman "Anna
Karénine".
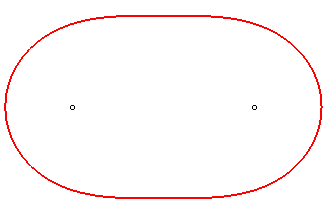
Pour (
),
l'ovale tend vers une forme circulaire quand
e tend vers l'infini.
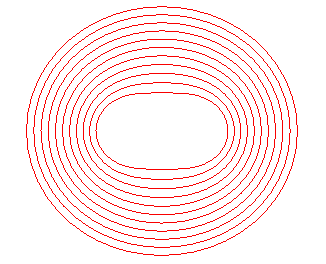
Dans le cas e < 1, l'équation
se met aussi sous la forme
,
où
et
(théorème
de Wangerin lien
page 19).
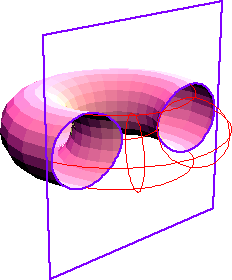
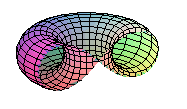
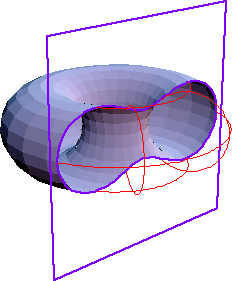
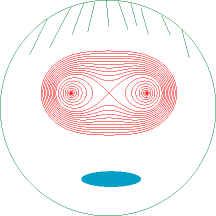
Les ovales de Cassini sont aussi les sections du tore
par les plans parallèles à l’axe situés à une
distance de l'axe égale au rayon mineur du tore (ici, section d’un
tore de rayon majeur R = a et de rayon mineur
par un plan situé à une distance r de l'axe - le tore
est donc croisé pour
)
; voir à
spirique
de Persée.
 |
 |
 |
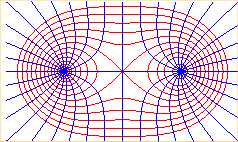
Les lignes de champ du champ magnétique créé par deux fils parallèles parcourus par un courant de même intensité et de même sens sont, dans chaque plan orthogonal aux fils les ovales de Cassini de foyers les points d'intersection avec les fils ; idem pour les équipotentielles du champ électrostatique créé par deux fils parallèles uniformément chargés avec des charges identiques.
Les trajectoires
orthogonales des ovales de Cassini sont les hyperboles équilatères
d'équation polaire
; ce sont les lignes de champ électrostatique dans l'interprétation
physique ci-dessus.
Si dans la définition des ovales de Casini on remplace la moyenne géométrique par la moyenne arithmétique on obtient les ellipses, et si on la remplace par la moyenne harmonique, on obtient les ovales de Cayley.
Voir la généralisation plane que constituent les cassiniennes, et les généralisations à l'espace que constituent les surfaces de Cassini. Comparer aussi avec les courbes de Booth.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2023