Courbe étudiée par Puiseux en 1844 et par Pirondini en 1892 et 1905, qui lui a donné son nom. Geminiano Pirondini : 1857 - 1914 : mathématicien italien.

 
 

Equation intrinsèque 1 :  avec n réel différent de –1. Equation intrinsèque 2 : . Paramétrisation cartésienne : . Abscisse curviligne : s = at. Rayon de courbure : .

La pseudo-spirale (de Pirondini) d'indice n est la courbe dont la courbure est proportionnelle à la puissance n-ième de l'abscisse curviligne. C'est une généralisation de la clothoïde (cas n = 1), renfermant aussi les cas du cercle (n = 0), de la spirale logarithmique (n = –1), de la développante de cercle (n = –1/2), et d'un cas limite d'alysoïde (n = –2).

Elle prend, pour t > 0, les formes suivantes :
 

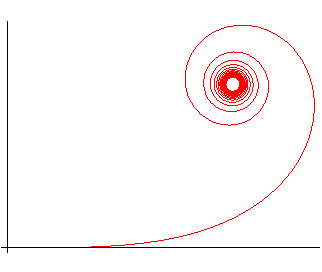
n > 0

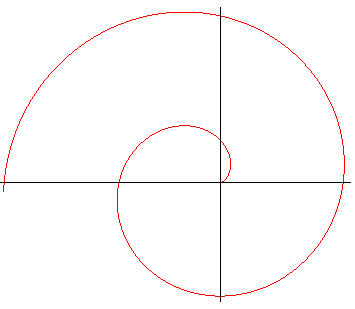
-1 < n < 0

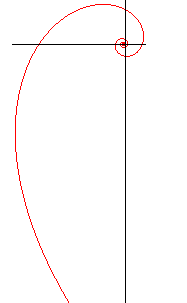
n < -1

Une propriété importante, expliquant le cas de la développante de cercle, est que la développée de la pseudo-spirale d'indice n est une pseudo-spirale d'indice  (équation intrinsèque ).
La radiale de la pseudo-spirale d'indice n est la spirale archimédienne d'indice , .

Sa courbe de Mannheim est la courbe d'équation cartésienne : .
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2012