Paramétrisation polaire :   où  ;  on a (voir les angles dans la figure ci-dessous). Équation polaire : . Équation polaire lorsque a = c : . Équation cartésienne de {0}: . Sextique tricirculaire,elliptique.

Une courbe de Watt est le lieu du milieu de la bielle [PQ] d'un quadrilatère articulé (APQB) vérifiant AP = BQ , A et B étant fixes - c'est donc un cas particulier de courbe du trois-barres à manivelles de même longueur ; ici, A(0, a), B(0, –a), AP = BQ = b, PQ =2c.

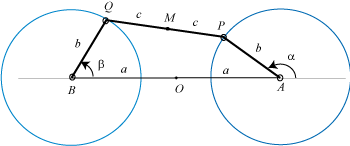
Autrement dit, une courbe de Watt est le lieu du milieu d'un segment de longueur constante joignant deux cercles de même rayon (les cercles (C_A) et (C_B) de centres A et B et de rayon b) ; penser par exemple au milieu d'une bielle joignant deux roues.

La courbe est non vide ssi .
 
 

La courbe passe par O ssi a, b, c sont les côtés d'un triangle, c'est-à-dire , soit  ; le point O est alors à la fois point double et point d'inflexion de chaque branche, qui est alors presque rectiligne au voisinage de O. Si l'on cherche les points où les tangentes en O recoupent la courbe, on trouve que ces points sont confondus avec O (autrement dit, que le contact est d'ordre deux) lorsque . Watt qui recherchait pour les mécanismes des machines à vapeur à obtenir un mouvement le plus rectiligne possible a construit son mécanisme dans ce dernier cas, qui présente de plus l'intérêt que si les deux barres AP et BQ sont horizontales au passage de M en O, la barre QP est verticale. L'intérêt d'obtenir un mouvement rectiligne par système articulé est d'éviter les frottements dus aux glissières, sources d'usure.

Mécanisme de Watt : a = 5, b = 4, c= 3.

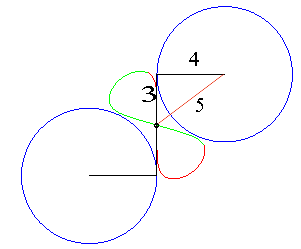
Lorsque la bielle [PQ] a même longueur que la barre fixe [AB] (c = a) , la courbe se décompose en la réunion du cercle (O, b) (cas où (APQB) est un parallélogramme), et d'une courbe de Booth ; on obtient un ovale si b > 2a , deux cercles si b = 2a (cas où le quadrilatère est un carré), une lemniscate si b < 2a, qui est de Bernoulli quand  .
NB : dans les animations ci dessous, P parcourt (C_A) à vitesse constante, ce qui provoque des saccades sur le parcours de Q sur (C_B).

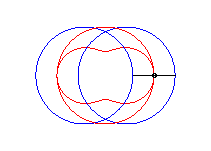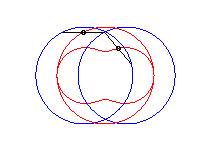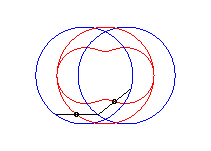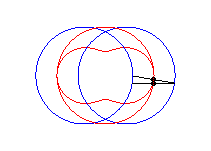
cas a = c < b/2 : ovale de Booth + cercle

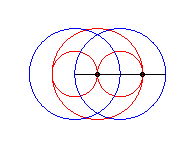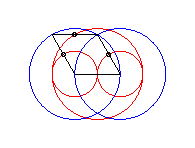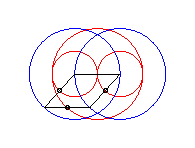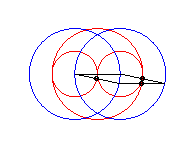
cas a = c = b/2 : trois cercles; pour les deux petits cercles rouge, le quadrilatère articulé est entièrement replié sur lui-même

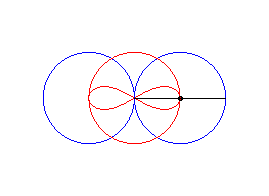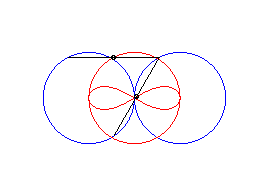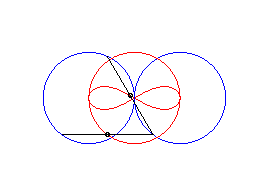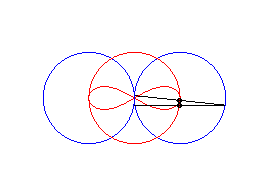
cas a = c > b/2 : lemniscate de Booth + cercle

D'une façon générale, le passage par O est obtenu pour , formule donnant aussi les angles polaires des tangentes correspondantes. On remarque que si d = 0, soit , les deux tangentes sont alors confondues.

Dans le cas  les courbes prennent donc les formes suivantes :
 

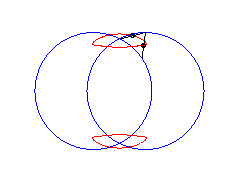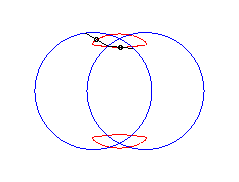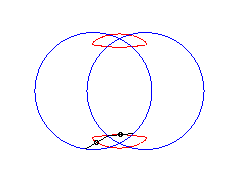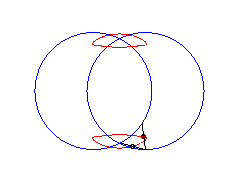
b > a + c et c < 2a :  courbe ayant deux composantes

:  courbe à deux croisements

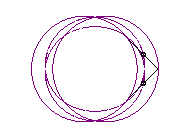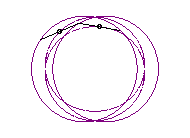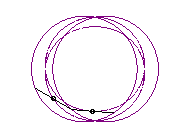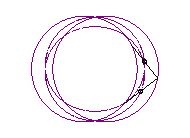
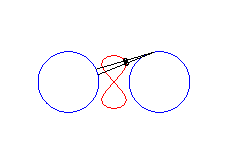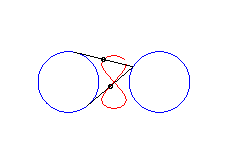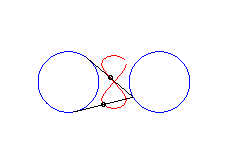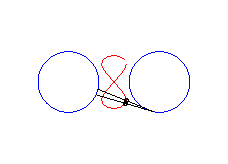
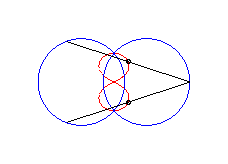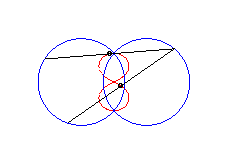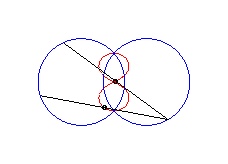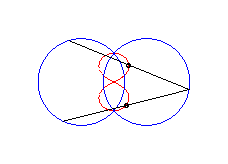
|a-b| < c < a : huit vertical

 

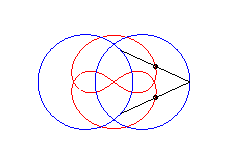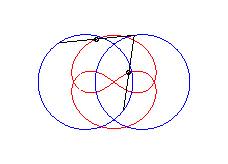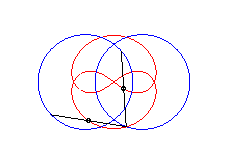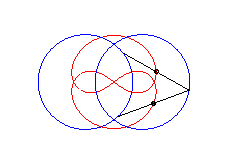
:  courbe à trois croisements.

: huit vertical avec croisement tangent.

: huit vertical.

 

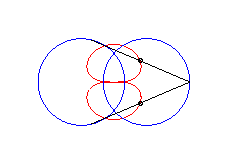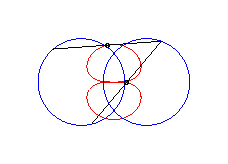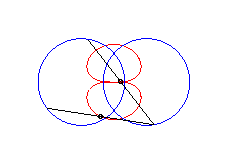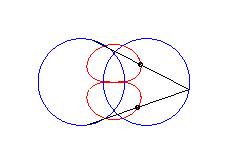
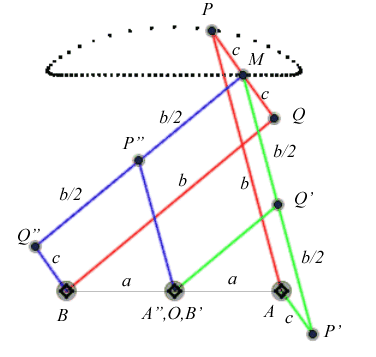
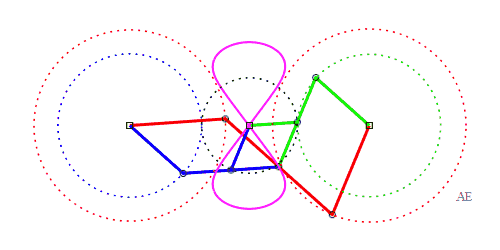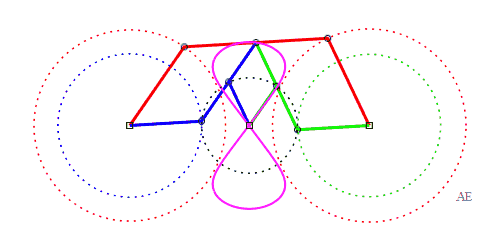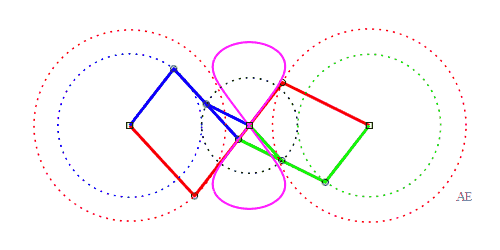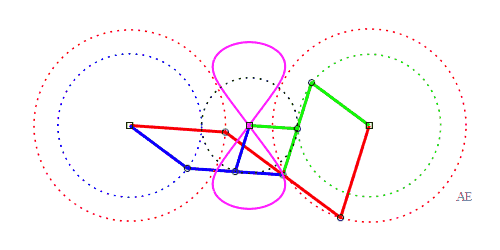
Le principe de triple génération des courbes du trois-barres s'applique aux courbes de Watt. Dans la figure ci-contre, le point P' est tel que AP'MP est un parallélogramme, et Q" est tel que BQMQ" est un parallélogramme. Le trois-barres normal (en rouge) est APQB, mais la même courbe est obtenue par le trois-barres AP'Q'O (en vert) et le trois-barres OP"Q"B (en bleu) ; cette fois, Q' est le milieu de [P'M], et P" est le milieu de [Q"M].

Exemple : trigénération du mécanisme de Watt.

Dans le cas où la courbe a deux composantes connexes, les 2 points d'intersections avec l'axe de symétrie médians ont une courbure nulle si ; dans le cas a = 2 , c = 1 on a b = ; l'approximation avec une droite est alors meilleure qu'avec le dispositif de Watt.

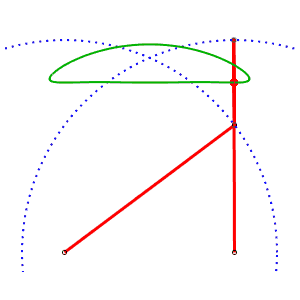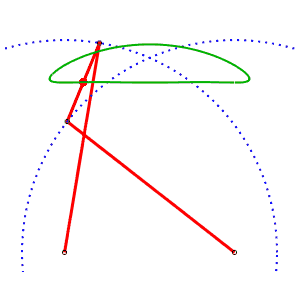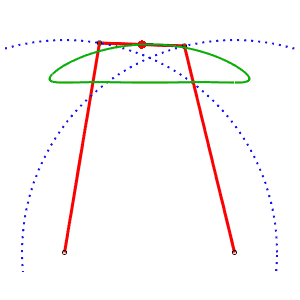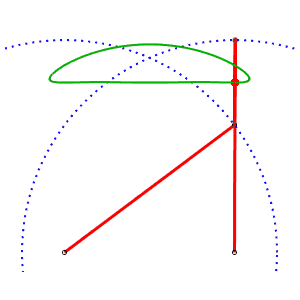
Mécanisme ou "cheval" de Tchébychef. AB = 4, AP = BQ = 5, PQ = 2, M milieu de [PQ]

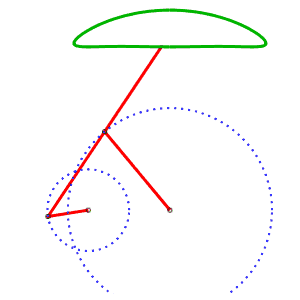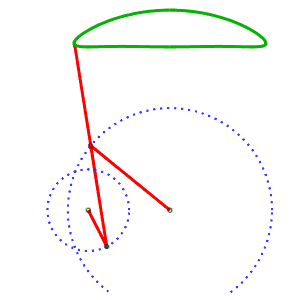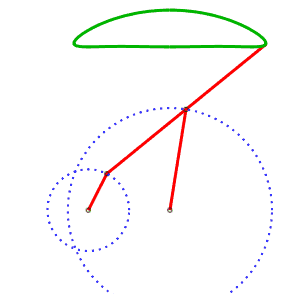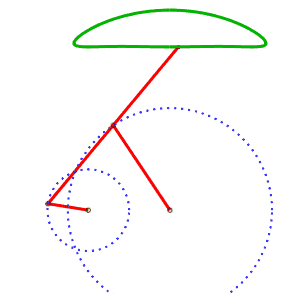
La génération alternative de la même courbe permet d'avoir un mécanisme où les courbes ne se croisent pas. AB = 4, AP = 5, BQ = 2, PQ = 5, P milieu de [QM]

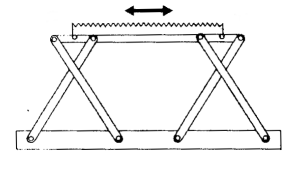
Scie utilisant le mécanisme de Tchebycheff Voir sur ce site russe, de belles animations du mécanisme de Tchébychev.

Mais voici ce que devient la partie pseudo-rectiligne après élongation des ordonnées :

Voir aussi le mécanisme de Roberts à courbe du trois-barres.
 

Un mouvement mathématiquement rectiligne obtenu par système articulé nécessite au moins 5 barres mobiles et est obtenu en particulier avec le mécanisme de Hart, ou l'inverseur de Peaucellier.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2021