| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE, OVALE, LEMNISCATE DE BOOTH
Curve,
oval, lemniscate of Booth ; Kurve, Oval, Lemniskate von Booth
|
|
|
| Courbes étudiées par Fagnano en 1750, Euler
en 1751, et Booth en 1877.
James Booth (1810 -1878 ) : mathématicien anglais. Autres noms : hippopède de Proclus, lemniscate elliptique (pour les ovales) et lemniscate hyperbolique (pour les lemniscates). |
Équation cartésienne : 
;
avec e = 1 pour les ovales (prendre 0 <  ),
e
=
–1 pour les lemniscates.
Quartique bicirculaire rationnelle. Équation polaire : Équation tripolaire : avec |
Les courbes de Booth sont les quartiques bicirculaires rationnelles ayant un centre de symétrie.
Comme toute quartique bicirculaire rationnelle, elles ont quatre définitions équivalentes :
1) Ce sont les podaires
de coniques à centre par rapport à leur centre (ici podaire
par rapport à
O de la conique 
).
-
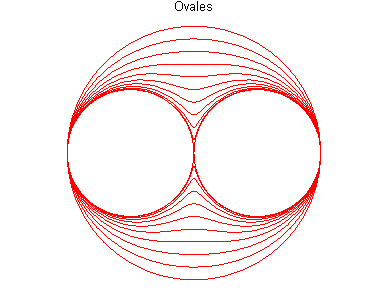
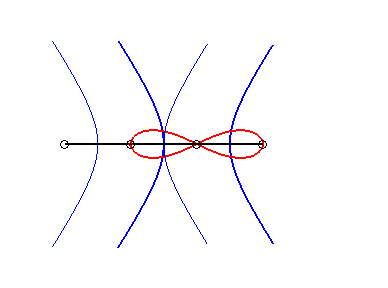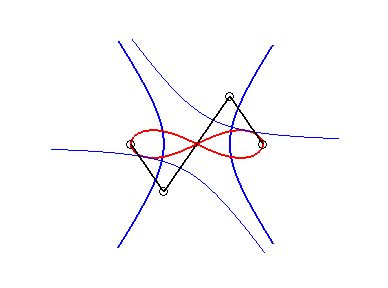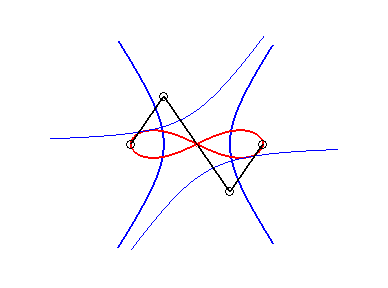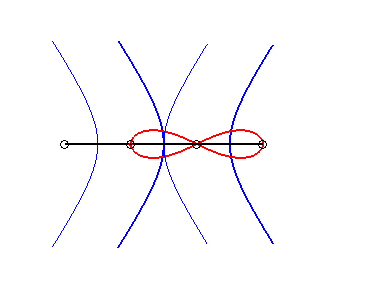
- Pour une ellipse, la courbe de Booth
est appelée
ovale de Booth ; ce ne sont de véritables
ovales (i.e. convexes) que pour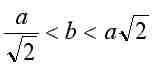 
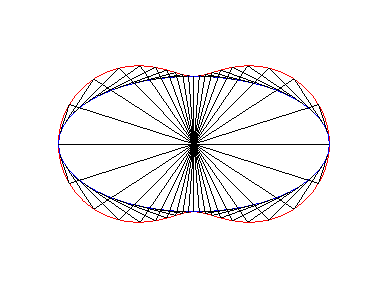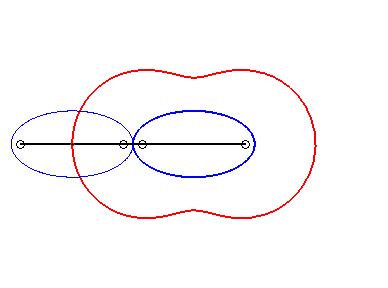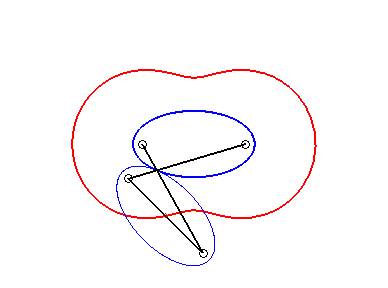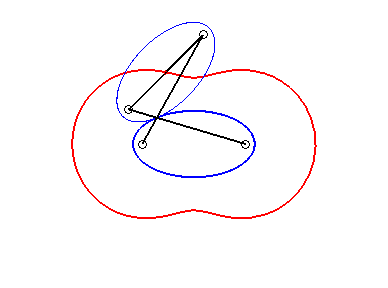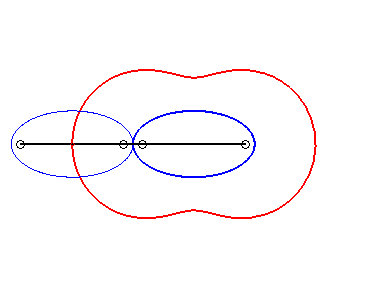
(et c'est un cercle pour a = b) ; elle a une
forme de haricot dans les autres cas.
 |
On en déduit que les ovales de Booth sont les lieux du centre d'une ellipse roulant sans glisser sur une ellipse égale, avec des sommets coïncidants, et donc aussi une courbe du trois-barres (voir plus loin l'interprétation en courbe de Watt) |
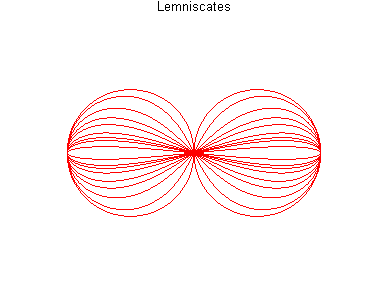
- Pour une hyperbole, elle est appelée
lemniscate
de Booth, à cause de sa forme de huit. On obtient une lemniscate
de Bernoulli lorsque l'hyperbole est équilatère.
 |
 |
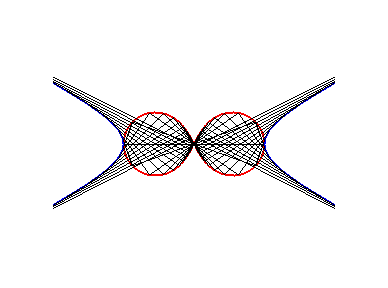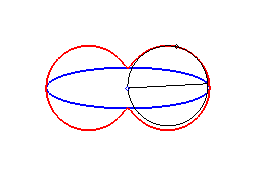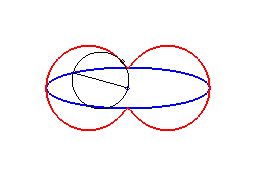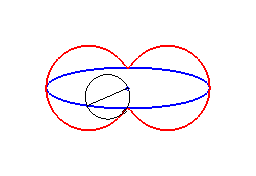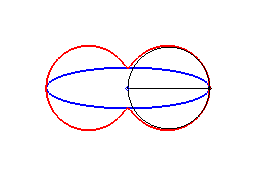
2) Ce sont donc les enveloppes de cercle de diamètre joignant le centre d'une conique à un point de cette conique.
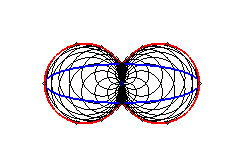
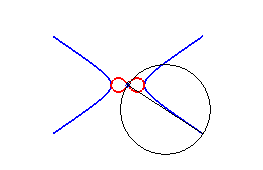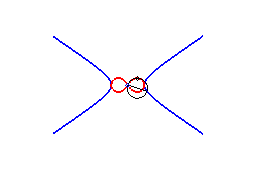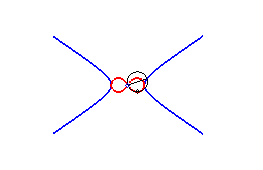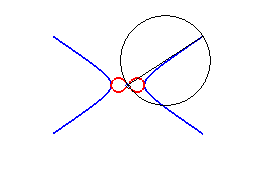
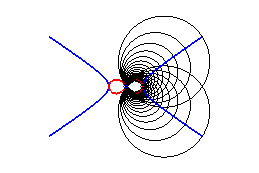
3) Ce sont les inverses
de coniques à centres par rapport à leur centre (ici, de
la conique 
,
si l'on prend ab comme puissance d'inversion - noter l'interversion
de
a et b par rapport à 1).
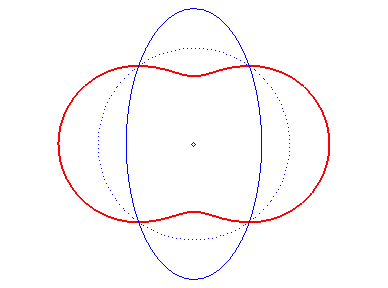
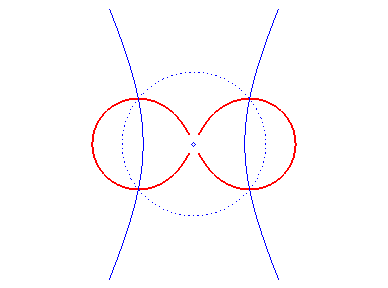
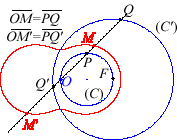
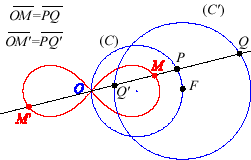
4) Ce sont les cissoïdales
de deux cercles (C) et (C') par rapport à un point
O,
tels que O appartient à (C) et le centre de (C')
est le point F de (C) diamétralement opposé
à
O. Le point F est l'un quelconque des foyers de
la conique du 1) ; ici par exemple F
, (C') étant de rayon a.
 |
 |
Mais elles possèdent 4 autres définitions
remarquables :
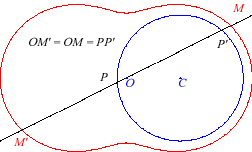
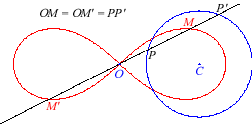
5) Ce sont les cissoïdales
de deux cercles confondus relativement à un point quelconque. On
obtient un ovale ou une lemniscate selon que le point est intérieur
ou extérieur au cercle. On obtient la lemniscate
de Bernoulli lorsque le point est à distance 
fois le rayon du cercle.
Ici, le cercle est le cercle de centre 
(milieu de [OF] ) et de rayon a/2.
|
|
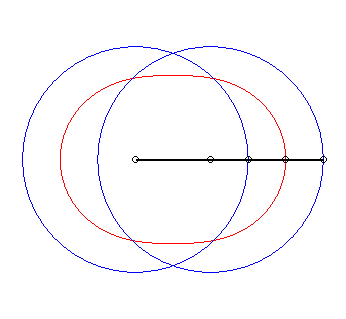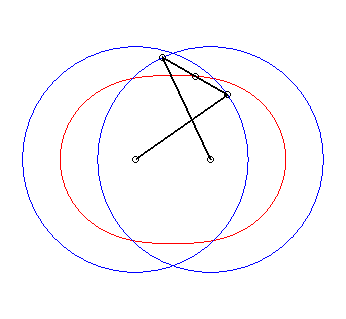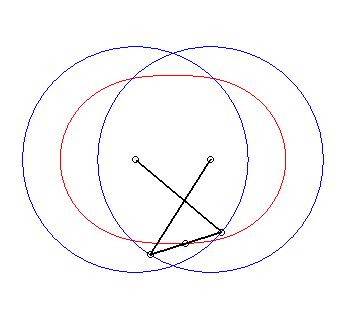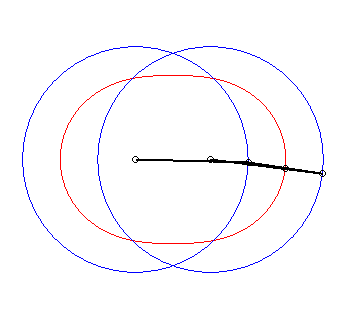
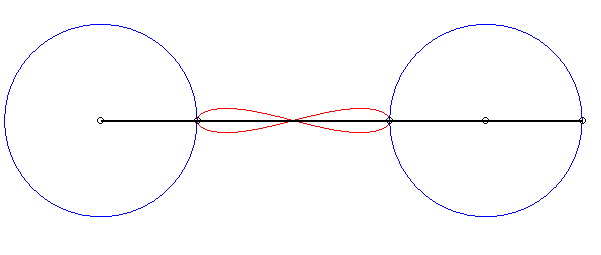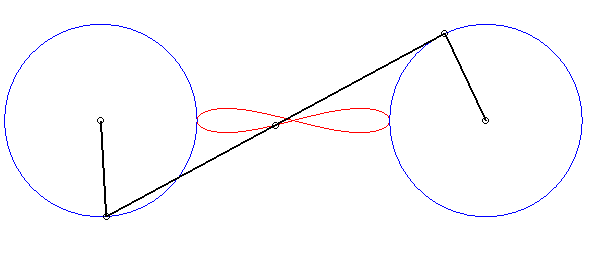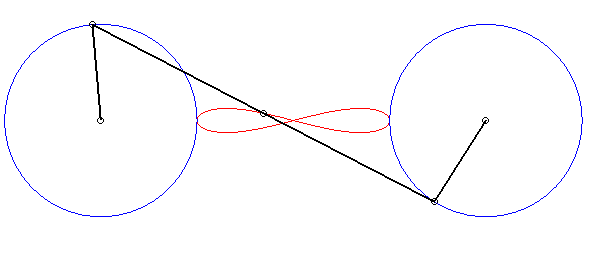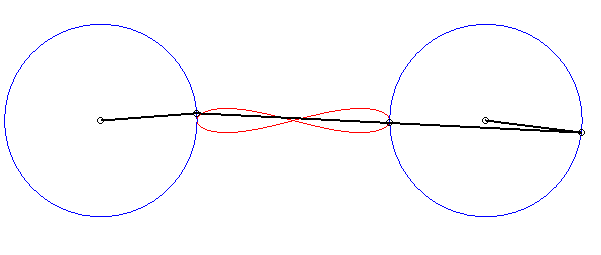
6) Ce sont des cas particulier de courbes
de Watt ; ce sont les lieux du milieu d'un segment de longueur 2d
joignant deux cercles de rayon a dont les centres sont distants
de 2d ; autrement dit, ce sont les lieux du milieu d'un côté
(de longueur 2d) d'un "rectangle" articulé, l'autre côté
(de longueur a) étant fixe ; on obtient les lemniscates lorsque
le grand côté est fixe, et les ovales dans l'autre cas.
 |
 |
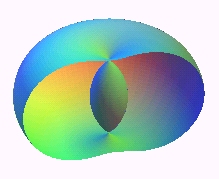
7) Ce sont les spiriques
de Persée (i.e. sections d'un tore par un plan parallèle
à son axe) lorsque le plan est tangent intérieurement au
tore. C'est à cause de cette définition que ces courbes sont
aussi appelées hippopèdes de Proclus.
Plus précisément, ce sont les sections
d'un tore de centre
O, d'axe Oz, de rayons majeurs et mineurs
a
et b coupé par le plan parallèle à
Oz situé
à une distance d =|a - b| de O
; la courbe est un ovale quand le tore est croisé (b > a)
et une lemniscate lorsqu'il est ouvert (a < b).
Dans un repère d’origine le projeté de O sur le plan, on obtient l'équation cartésienne :
.
 |
 |
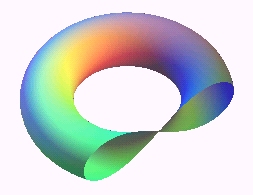8) Ce sont les projections sur xOy des biquadratiques
intersections du paraboloïde de révolution 
avec le cône du second degré 
.
9) Si l'on effectue une affinité 
sur l'ovale 
,
on obtient la courbe d'équation polaire 
avec 
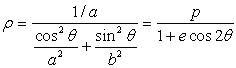
et 
; les ovales de Booth sont donc, à affinité près,
des
polygastéroïdes.
Comparez les courbes de Booth avec les ovales de Cassini.
Voir aussi la surface
d'élasticité de Fresnel, qui est la généralisation
à l'espace de l'ovale de Booth.
Voir aussi les lemniscates de Booth sur la surface
romaine.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2008
.
dans
le tripôle (F, F',O) où F(d,0)
et F'(–d,0),
,
.
( 
, 
)
(
pour l'ovale, 
pour la lemniscate. 
