COURBE D'ARCHYTAS
Archytas
curve, Kurve des Archytas
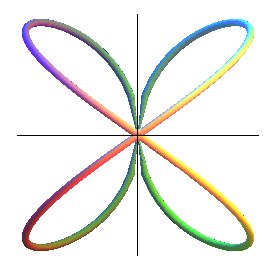
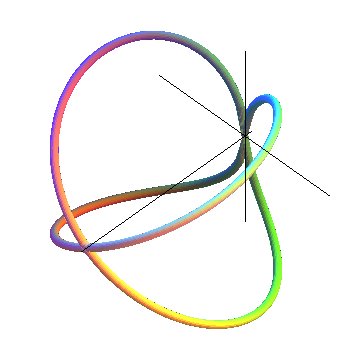
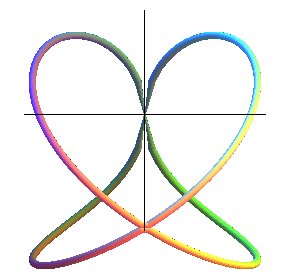
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE D'ARCHYTAS
Archytas
curve, Kurve des Archytas

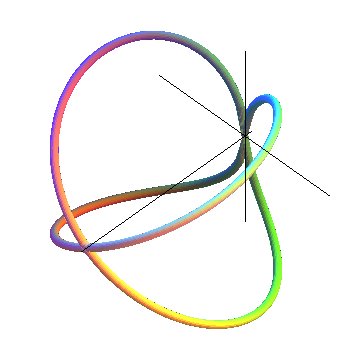
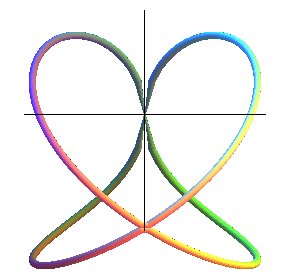
| Archytas
de Tarente (430-350 avant J.C.) : général, savant et
homme d'état grec.
Cette courbe serait la première courbe non plane historiquement considérée. Page internet : www.mathouriste.eu/Delos/Delos_pb3.html |
| Système díéquations cartésiennes
: Système d'équations cylindriques : Système d'équations sphériques : Courbe algébrique de degré 8 (biquartique 3D). Paramétrisation cartésienne : |
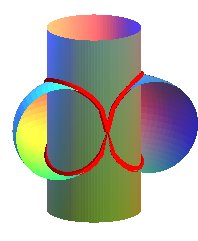
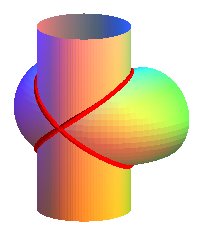
| La courbe d'Archytas est la courbe intersection d'un tore à trou nul avec un cylindre de révolution d'axe perpendiculaire au cercle central du tore, et de même rayon que lui. |
 |
 |
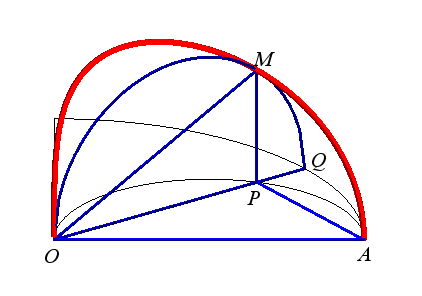
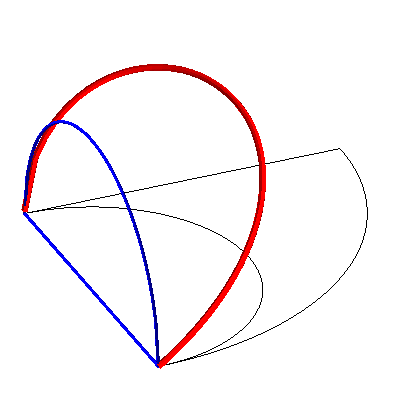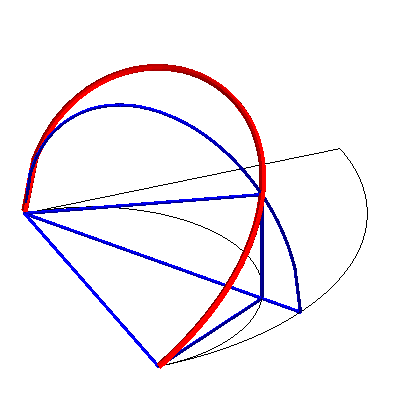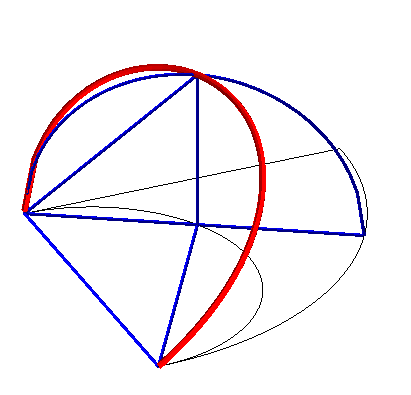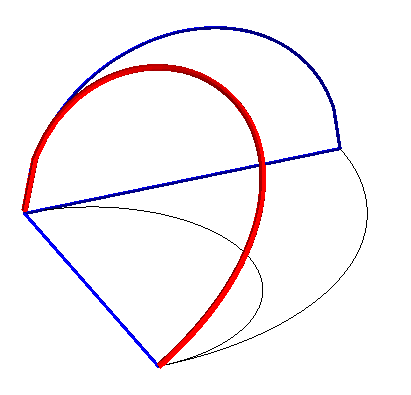
| Construction de la courbe :
Le tore est engendré par un cercle (CQ) de diamètre horizontal [OQ], le point Q ayant un mouvement circulaire autour de O, et le cylindre, par une droite (D) verticale passant par P, le point P décrivant un cercle fixe de diamètre [OA] (OQ = OA). Prenant P sur (OQ), le point M d'intersection de (D) avec (CQ) décrit la courbe d'Archytas. Analytiquement : La latitude |
 |
 |
Elle a été considérée par
Archytas car c'est une duplicatrice
:
en effet, 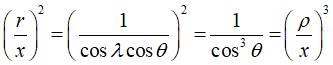
,
; dans cette configuration, les deux nombres
et
apparaissent
simultanément comme des rapports de longueurs, mais pour obtenir
cette configuration, il faut connaitre
qui n'est pas constructible.
| On peut généraliser au cas du tore à
trou non nul : intersection du tore Lorsque a augmente, la courbe tend vers une bicylindrique (cas de la double ellipse). |
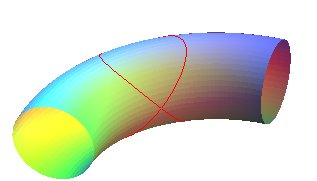 |
Comparer avec les bitoriques.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2023