Famille	polyèdre semi-régulier ou polyèdre d'Archimède également : paralléloèdre
Historique	solide connu d'Archimède (IIIe s. av. J.C.)
Dual	Tétraki-hexaèdre
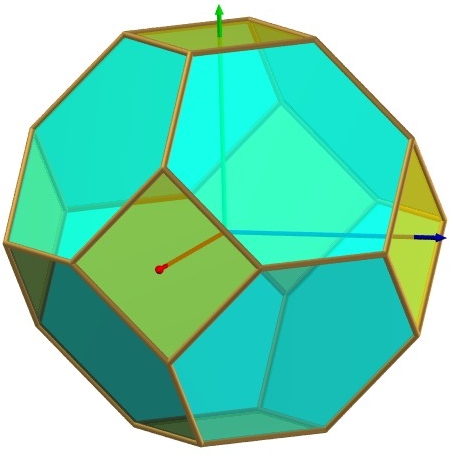
Faces	8 hexagones et 6 carrés ; c'est donc un tétradécaèdre, parfois dénommé aussi tétrakaidécaèdre.
Sommets	24 sommets de degré 3, de code de Schläfli 4.62 .
Arêtes	36 arêtes de longueur a ; angle dièdre : = 125° 15' 52"  entre un carré et un hexagone,  entre deux hexagones.
Patron et graphe
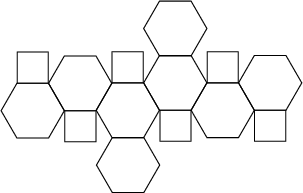Diamètres	sphère inscrite dans les hexagones : , dans les carrés :  intersphère (passant par les milieux des arêtes) : 3a ; sphère circonscrite : .
Mensurations	volume :     aire :  coefficient isopérimétrique :
Coordonnées  des sommets	et les permutés, avec.
Constructions	octaèdre faiblement tronqué aux sommets : (la troncature finale est le cuboctaèdre) cube tronqué aux arêtes et fortement tronqué aux sommets : (la troncature intermédiaire est le cuboctaèdre tronqué) tétraèdre tronqué aux arêtes et fortement tronqué aux sommets : (la troncature finale est le tétraèdre tronqué)
Plans de symétrie	9
Axes de rotation	3 axes passant par les centres de 2 carrés opposés (2 rotations d'ordre 4  par axe et une d'ordre 2) 4 axes passant par les centres de 2 carrés opposés (2 rotations d'ordre 3  par axe) 6 axes passant par les milieux de deux arêtes communes à des hexagones et opposées (1 rotations d'ordre 2  par axe)
Groupe des isométries	= celui de l'octaèdre
Polyèdre dérivé	Triacontahexaède tétragonal

Comme avec des cubes, on peut paver (c'est-à-dire remplir sans trou ni chevauchement) l'espace avec des octaèdres tronqués. Voir aussi paralléloèdre. Nota 1 : la surface d'équation implicite :  est formée d'un tel réseau d'octaèdre. Nota 2 : une version arrondie de ce réseau d'octaèdres est la surface P de Schwarz.

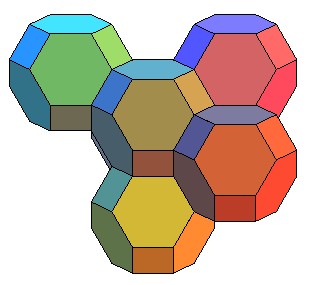Le réseau de cordes de cette pyramide est un empilement compact d'octaèdres tronqués

Cette propriété d'empilement sans interstice provient du fait que l'octaèdre tronqué n'est autre que le "domaine fondamental" (à savoir le domaine formé des points pour lesquels le nœud le plus proche est le nœud considéré) d'un réseau cubique centré (voir ci-dessous). Ci-contre, les cuboctaèdres sont centrés aux points de coordonnées , avec i,j,k entiers de même parité.

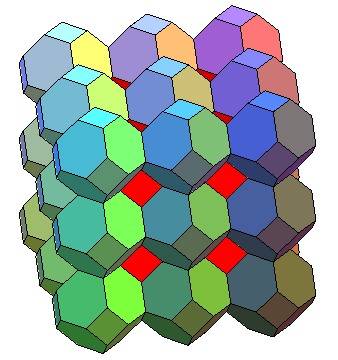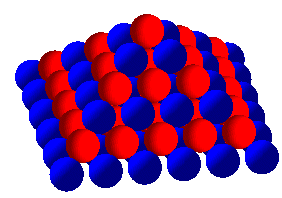
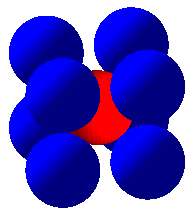
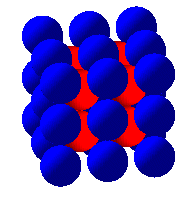
Le réseau cubique centré est obtenu à partir de deux réseaux cubiques simples, chaque nœud de l'un étant au centre d'un cube formé par 8 nœuds de l'autre. On définit la densité d'un réseau comme la limite du rapport du volume total des sphères identiques tangentes centrées aux noeud du réseau situées dans un domaine donné, au volume du domaine, lorsque le domaine "tend" vers l'espace entier. Il se trouve que le réseau cubique centré est moins dense (densité ) que le réseau cubique à faces centrées, dont le domaine fondamental est le dodécaèdre rhombique.

Le cube, l'octaèdre tronqué, et le dodécaèdre rhombique pavent l'espace, mais des 3, c'est l'octaèdre tronqué qui a le coefficient isopérimétrique le plus élevé, ce qui signifie que pour un volume donné, c'est lui qui a la surface extérieure la plus petite. Lord Kelvin pensait que de tous les pavages de l'espace par des cellules identiques (non forcément polyédriques), celui qui avait le coefficient isopérimétrique le plus élevé était le pavage par un octaèdre tronqué légèrement modifié. Ceci a été démenti par la découverte de la mousse de Weaire-Phelan qui a un meilleur coefficient, elle-même détronée en 2016 (voir wikipedia).
 

Il ne faut pas confondre l'octaèdre tronqué avec le dodécaèdre rhombique tronqué représenté ci-contre, qui s'obtient lui aussi par troncature du cube, possède aussi 6 faces carrées et des faces hexagonales, mais celles-ci sont au nombre de 12 au lieu de 8 et ne sont mêmes pas régulières. Noter aussi aussi les deux types de sommets.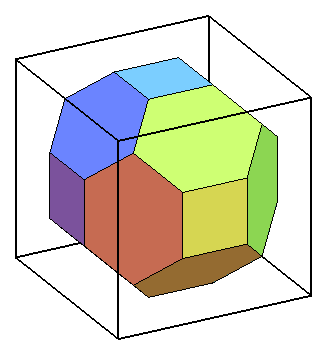

 

Je pense que ce polyèdre réalisé avec 24 tickets de métro que j'ai acheté à une personne qui les vendait sur un quai a la structure d' un octaèdre tronqué. Les 4 tickets du haut délimitent une des faces carrées, les 3 tickets de gauche en triangle sont 3 arêtes d'une des faces hexagonales.

 

Pavage par des octaèdres tronqués photographié par Carlos Sacré, en Roumanie près de Constanza.	Pavage par des octaèdres tronqués séparés par des prismes. Structure du cristal de faujasite.	Horloge solaire du 16ème siècle (musée Galilée, Florence)

 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2017