CUBOCTAÈDRE
Cuboctahedron, Kuboktaeder
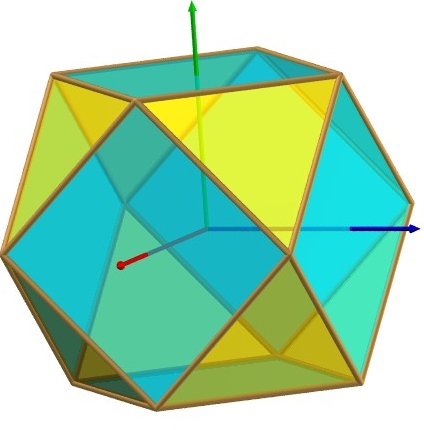
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CUBOCTAÈDRE
Cuboctahedron, Kuboktaeder

| De cube et octaèdre (vient du fait que c'est l'intersection
d'un cube et d'un octaèdre) ; nom donné par Képler.
Autre nom : dymaxion (donné par Buckminster Fuller). Vues Povray de cette page réalisées par Alain Esculier. Lien : mathematische-basteleien.de/kuboktaeder.htm Octaèdre articulé transformé en cuboctaèdre : demonstrations.wolfram.com/HingedOctahedron/ |
| Famille | polyèdre semi-régulier ou polyèdre d'Archimède | ||||||
| Historique | solide connu de Platon | ||||||
| Dual | dodécaèdre
rhombique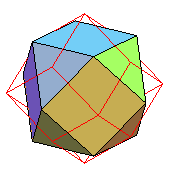 |
||||||
| Faces | 8 triangles et 6 carrés ; c'est donc un tétradécaèdre. | ||||||
| Sommets | 12 sommets de degré 4, de code de Schläfli 3.4.3.4 . | ||||||
| Arêtes | 24 arêtes de longueur a ; angle dièdre
: |
||||||
| Patron |
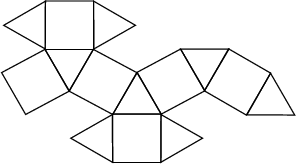 (6912
patrons en tout) (6912
patrons en tout) |
||||||
| Graphe |
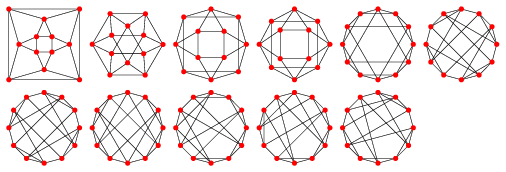 |
||||||
| Diamètres | sphère inscrite dans les carrés : intersphère (tangente aux arêtes) : |
||||||
| Mensurations | volume : |
||||||
| Coordonnées
des sommets |
|||||||
| Équations des 14 plans faces
d'où : équation cartésienne de la surface |
les 6 carrés : d'où l'équation : |
||||||
| Équations des 4 plans passant par O contenant
les arêtes,
d'où : équation cartésienne de la surface |
d'où l'équation : |
||||||
| Constructions |
   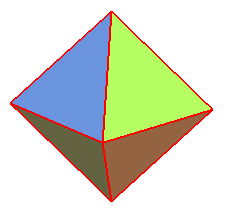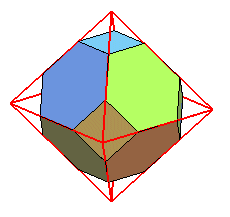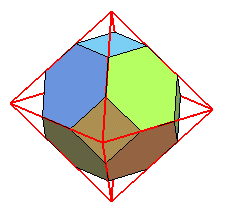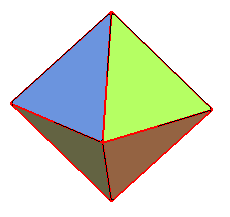 |
||||||
| Polyèdres dérivés | par troncature
faible modifiée : rhombicuboctaèdre
;
par troncature forte modifiée : cuboctaèdre tronqué ; par augmentation : icositétraèdre trapézoïdal. Voir aussi l'octahémioctaèdre et le cubohémioctaèdre, polyèdres étoilés qui ont les mêmes arêtes. |
||||||
| Plans de symétrie | les 3 plans contenant des diagonales de carrés opposés et les 6 plans contenant des hauteurs de triangles opposés. | ||||||
Axes de rotation
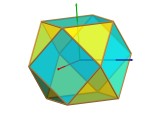 |
|
||||||
| Groupe des isométries | = celui du cube (ou de l'octaèdre). |
| Si l'on partage chaque face carrée en deux triangles de sorte que les 12 sommets deviennent de degré 5, on obtient un "polyèdre" équivalent à l'icosaèdre. | 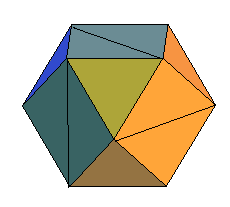 |
| Si on pose le cuboctaèdre sur une face triangulaire et si on fait pivoter la moitié supérieure ou inférieure d'un sixième de tour, on obtient un polyèdre qui n'est plus semi-régulier mais reste inscriptible à faces régulières, dénommé gyro-cuboctaèdre, ou pseudo-cuboctaèdre ou, suivant la terminologie de Johnson : orthobicoupole hexagonale (J 27). | 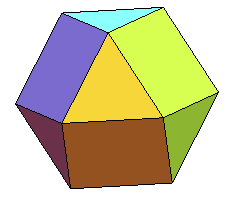 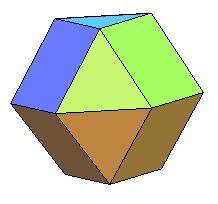 |
 |
Les 24 arêtes du cuboctaèdre se regroupent
en 4 hexagones réguliers.
Par projection centrale du squelette sur la sphère circonscrite, les 4 hexagones deviennent 4 grands cercles (cf. le même phénomène avec l'octaèdre et l'icosidodécaèdre). Si l'on entrelace ces cercles avec alternance dessus-dessous, on obtient un entrelacs premier à quatre composantes et 12 croisements. |
 |
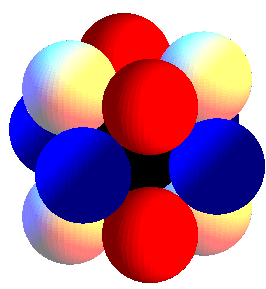 |
Le problème dit "de la treizième sphère",
ou "du nombre d'embrassades" (kissing number).
L'arête du cuboctaèdre étant égale
à son rayon, on peut placer 12 sphères de rayon 1 aux sommets
d'un cuboctaèdre de rayon 2, sans qu'elles ne se chevauchent. Ces
douze sphères étant tangentes à la sphère centrale
de rayon 1, ceci montre que l'on peut placer 12 sphères autour d'une
même sphère, toutes les sphères ayant même rayon
(voir aussi la solution icosaèdrique)
; cette disposition est d'ailleurs celle du réseau cristallin dit
"cubique à faces centrées" |
 |
Par projection, ce problème est équivalent à celui consistant à placer sur une sphère un nombre maximal de calottes sphériques d'angle au centre 60°. Le maximum est douze, mais la solution cuboctaédrique n'est pas la seule. Sources : Ian Stewart, Pour la Science 174, p. 102. et Marcel Berger, dossier Pour la Science 41 p. 68. |
Voici, gravé par Escher, puis réalisé avec le logiciel povray par Alain Esculier, le polyèdre composé du cube et de l'octaèdre dual dont le cuboctaèdre est l'intersection :

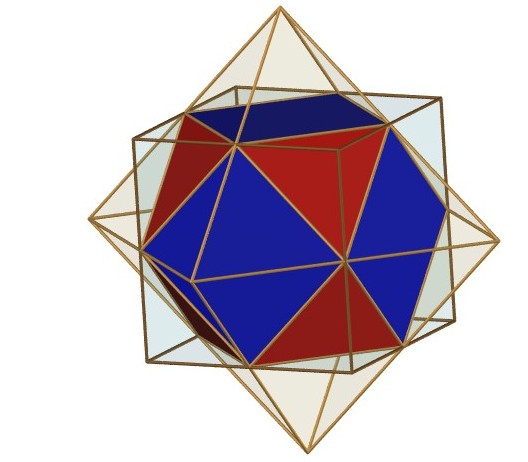
Voir aussi la surface
de Néovius, dont la cellule de base a une forme cuboctaédrique.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016