CASSINIAN OVAL
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CASSINIAN OVAL

| Curve studied by Cassini in 1680 and Malfatti in 1781.
Informal name: cat eyes. Jean-Dominique Cassini (1625-1712): French astronomer.
|
| Bipolar equation: Cartesian parametrization: Polar equation: the equation with " – " yielding real points only when e Cartesian equation: or even: Elliptic bicircular quartic (rational for e = 1).
Area of an oval for e < 1: |
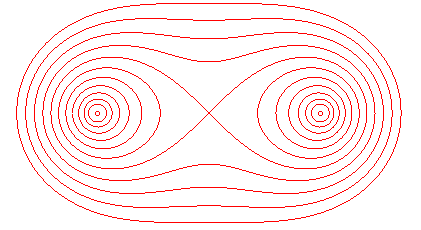
The Cassini ovals are the loci of the points on
the plane for which the geometric mean of the distances to two points,
the foci, is constant (= b).
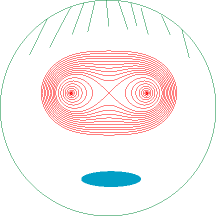
They also are the field
lines of the vector field ,
sum of two orthoradial 1/r fields.
In the case when e < 1 (b < a), the "oval" is composed of two curves shaped like symmetrical eggs with respect to O with tripolar equations:
In this case, the curve is anallagmatic:
invariant under the inversion of centre O and radius
; therefore we have a cyclic generation:
the initial curve is the hyperbola
with
and
,
and the inversion circle (with radius Öp)
is the Monge circle.

The Cassini oval as the envelope of the circles centred on a hyperbola and orthogonal to its Monge circle.
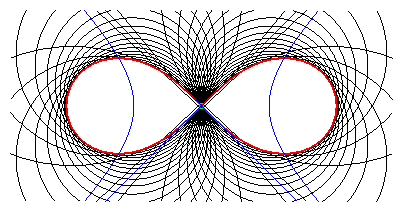
Here, the hyperbola is rectangular and the green circle reduces to
O.
In the case when e > 1, the real Cassini oval is no longer anallagmatic, but the complex curve still is, with a complex inversion radius.
For
(
): the oval
has the shape of an "ellipse" that is worn out at the summits of the minor
axis.
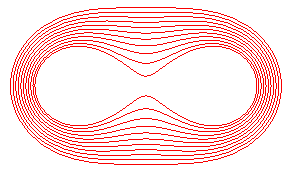
For ,
the oval finally has an oval shape. Valery
Ochkov proposes to baptize it "oval of Tolstoy" for its resemblance
with
Tsarskoye Selo hippodrome near Saint Petersburg, hippodrome
mentioned in the novel "Anna
Karenina".
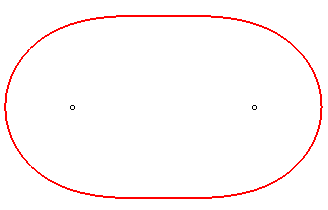
For (
):
the oval finally has an oval shape, leaning towards a circular shape as
e
increases to infinity.
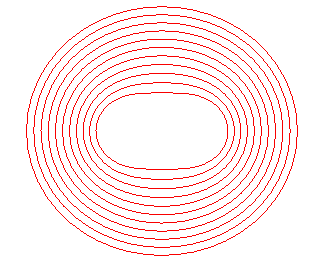
In the case when e < 1, the equation
can be written
,
where
and
(Wangerin's
theorem link
page 19).
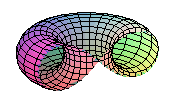
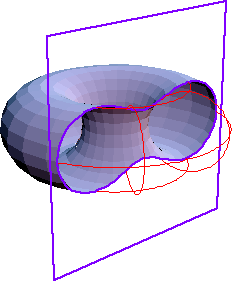
The Cassini ovals also are the sections of a torus by
planes parallel to the axis, located at a distance to the axis equal to
the minor radius of the torus (here, section of a torus with major radius
R
= a and minor radius
by a plane located at distance r to the axis - the torus is thus
a spindle torus for
)
; see spiric of Perseus.
 |
 |
 |
The field lines of the magnetic field created by two parallel wires carrying currents of equal intensity in the same direction are, in any plane orthogonal to the wires, the Cassini ovals with foci the intersection points with the wires. The same is true for the equipotential lines of the electrostatic field created by two uniformly charged parallel wires with identical charge.
The orthogonal
trajectories of the Cassini ovals are the rectangular hyperbolas with
polar equation
; they are the electrostatic field lines in the physical interpretation
above.
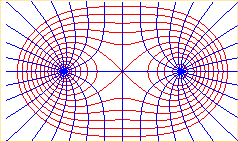
If, in the definition of the Cassini ovals, the geometric mean were replaced by the arithmetic mean, it would result in ellipses, and if it were replaced by the harmonic mean, it would yield Cayley ovals.
See the generalisation that are Cassinian curves, also compare with Booth curves and look at surfaces of Cassini.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017