Bielle de Bérard

COURBE DE LA BIELLE DE BÉRARD
Curve ot the slider-crank mechanism, Kurve der Schubkurbel

N'est représenté ci-dessus à gauche que la moitié de chaque courbe ; il faudrait les compléter par leur symétrique par rapport à (OA).

Courbe étudiée par Bérard en 1820 et Ruiz-Castizo en 1889.
Autres noms : courbe du système bielle-manivelle, quartique de Ruiz-Castizo.

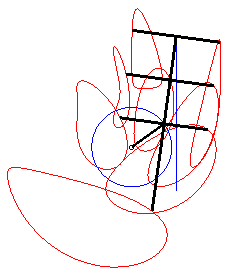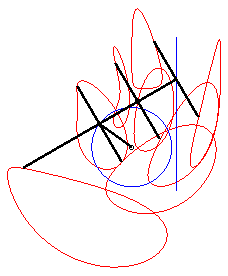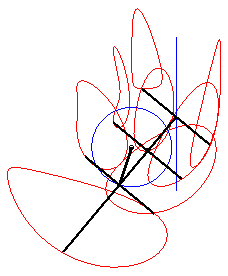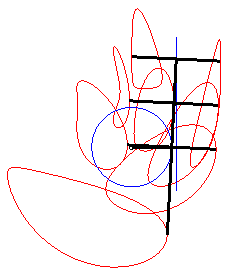
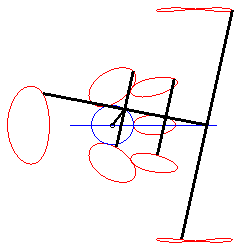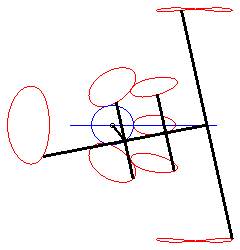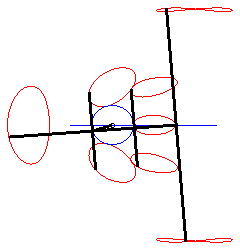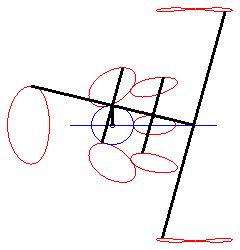
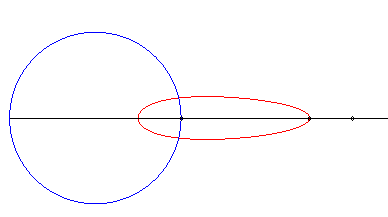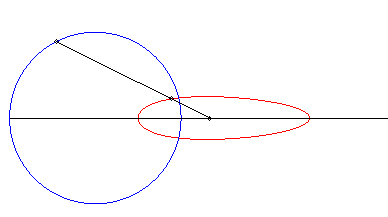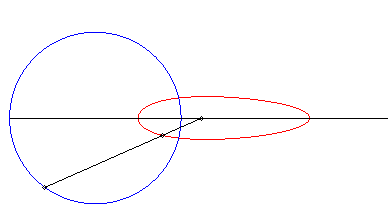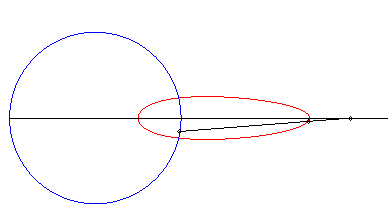
Une courbe de la bielle de Bérard est le lieu d’un point fixé M du plan lié à la barre [PQ] (appelée la bielle) d'un mécanisme articulé (OPQ), O étant fixe et Q astreint à se mouvoir sur une droite (D) (le tiroir, ou piston). Autrement dit, une courbe de la bielle de Bérard est le lieu d'un point lié à un segment de longueur constante joignant un cercle (C) à une droite (D).

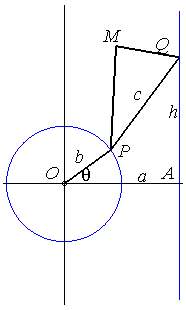Nous choisissons A(0, a) projeté de O sur (D) , OP = b, PQ = c.
En prenant des lettres minuscules pour les affixes des points, on a :

En écrivant , on obtient en prenant :
Paramétrisation cartésienne :
, avec avec suivant la position de Q par rapport à (OP) ;
en particulier, le mouvement de Q n'est pas sinusoïdal.
Quartique bicirculaire (?).
Beau schéma tiré du livre de Savelov p172

Équation cartésienne lorsque M est sur la droite (PQ) (soit l = 0) :
.
Aire : (obtenue par le théorème de Holditch) : elle ne dépend que de la dimension du cercle et de la position de M sur la bielle, pas de la longueur de celle ci. Savelov p173

La courbe est non vide si et seulement si a £ b + c, et dans ce cas, elle est connexe ssi b £ a + c (?).

Lorsque M est sur la bielle, l'équation ci-dessus montre que la courbe de Bérard est alors une courbe polyzomale, médiane des deux ellipses : , et .

En particulier :

- lorsque a = 0 ((D) passe par O) et k = -1, ces deux ellipses sont des cercles concentriques : les courbes associées sont les quartiques de Bernoulli. Voir sur cette page la base et la roulante du mouvement plan sur plan associé.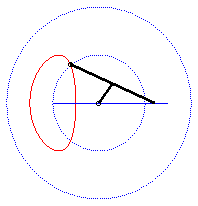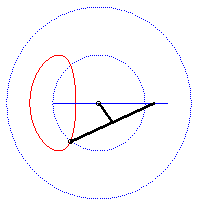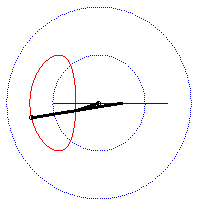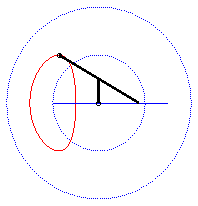

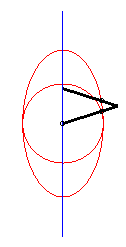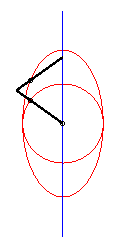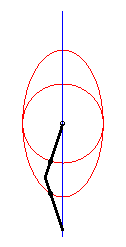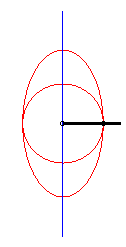
- lorsque c = a + b et k = -1, ces deux ellipses sont des cercles tangents : les courbes associées sont les doubles-coeurs.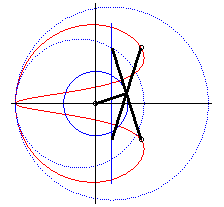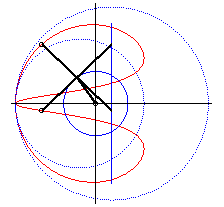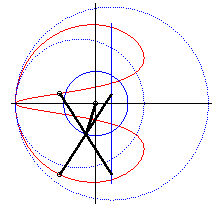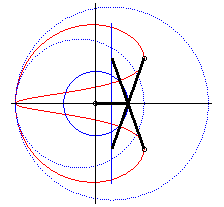

- lorsque a = 0 et b = c, la courbe de Bérard se décompose en un cercle et une ellipse (on retrouve en fait la construction de l'ellipse par la bande de papier).

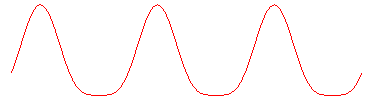
Le dispositif sert à créer un monvement rectiligne quasi sinusoïdal ; ci-contre la représentation du mouvement de Q pour a = 0, b = 1, c = 3.
Voir aussi une application à l'essuie-glace Mercédès.

Si on remplace le cercle (C) par une conique quelconque, on obtient toutes les courbes polyzomales.

Si on remplace la droite (D) par un cercle, on obtient une courbe du trois-barres.

Si la bielle n'est plus astreinte à ce que son extrémité coulisse sur une droite, mais à coulisser en passant par un point fixe, on obtient les conchoïdes de cercles.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

	Nous choisissons A(0, a) projeté de O sur (D) , OP = b, PQ = c. En prenant des lettres minuscules pour les affixes des points, on a : En écrivant , on obtient en prenant : Paramétrisation cartésienne : , avec avec suivant la position de Q par rapport à (OP) ; en particulier, le mouvement de Q n'est pas sinusoïdal. Quartique bicirculaire (?).	Beau schéma tiré du livre de Savelov p172
	Équation cartésienne lorsque M est sur la droite (PQ) (soit l = 0) : . Aire : (obtenue par le théorème de Holditch) : elle ne dépend que de la dimension du cercle et de la position de M sur la bielle, pas de la longueur de celle ci.	Savelov p173

- lorsque a = 0 ((D) passe par O) et k = -1, ces deux ellipses sont des cercles concentriques : les courbes associées sont les quartiques de Bernoulli. Voir sur cette page la base et la roulante du mouvement plan sur plan associé.
- lorsque c = a + b et k = -1, ces deux ellipses sont des cercles tangents : les courbes associées sont les doubles-coeurs.
- lorsque a = 0 et b = c, la courbe de Bérard se décompose en un cercle et une ellipse (on retrouve en fait la construction de l'ellipse par la bande de papier).