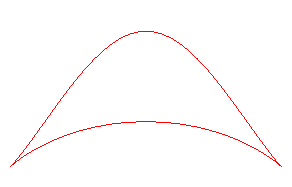
BICORNE
Bicorn
or cocked hat curve, Zweihornkurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
BICORNE
Bicorn
or cocked hat curve, Zweihornkurve

| Courbe étudiée par Sylvester
en 1864, Cayley en 1867 , Charlotte Scott en 1896 et G. de Longchamps
en 1897.
Nom donné par Sylvester. |
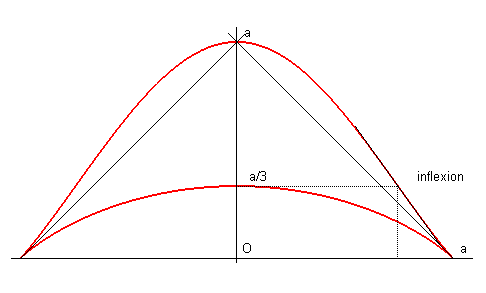 |
Équation cartésienne : Paramétrisation cartésienne : Abscisse curviligne : Longueur : Aire : Quartique rationnelle, circulaire. |
| Première construction (Charlotte
Scott, Intermédiaire des mathématiciens, 1896, p. 250)
Soient (C) et (C') deux cercles tangents, de centres O et O' et de rayon a ; un point N décrivant (C'), le bicorne est le lieu des points d'intersection de la parallèle à (OO') passant par N avec la polaire de N par rapport au cercle (C). |
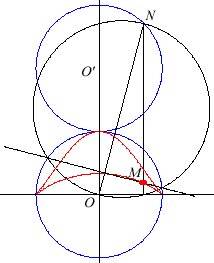 |
| Deuxième construction (G. de Longchamps, JMS,
1897)
Étant donné deux points fixes A(a,
0) et B(–a, 0), un cercle (C) de centre C(b,
c)
de rayon r et de point courant P, le lieu de l'orthocentre
H
du triangle ABP a pour paramétrisation : REM : pour a = b = c = 0, on obtient le
kappa,
si |
 |
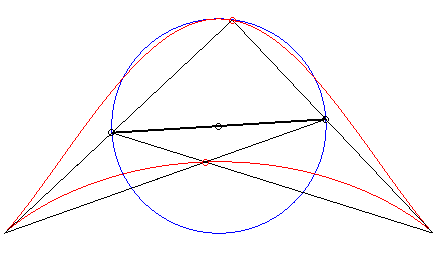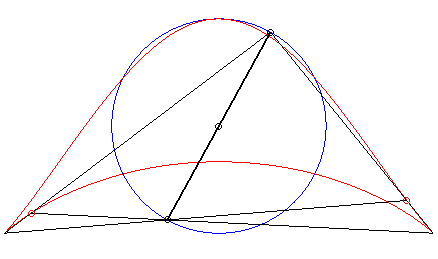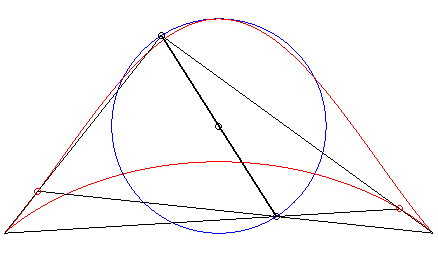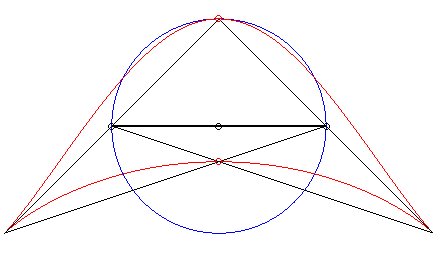
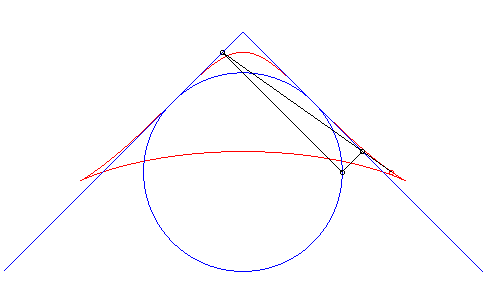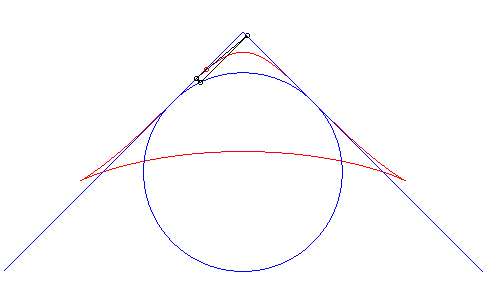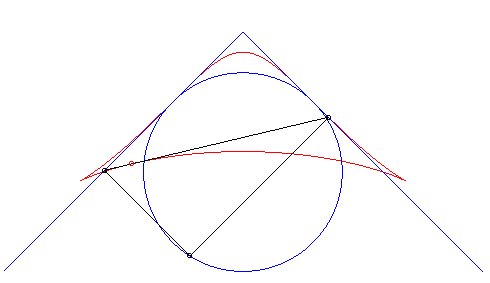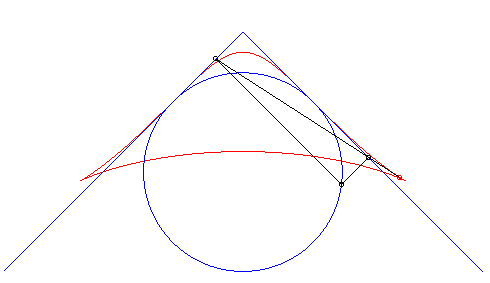
| Troisième construction (V. Jerabek, mathesis,
1912).
Étant donné deux points fixes A(a, 0) et B(–a, 0), un cercle (C) de centre C(0, b) de rayon c, et un diamètre variable [PQ] du cercle (C), le lieu des intersections des droites (AP) et (BQ) (ou (AQ) et (BP) ) a pour paramétrisation : Si M et N sont les points d'intersection des droites (AP) et (BQ) et des droites (AQ) et (BP), la droite (MN) enveloppe une cissoïde droite. Une généralisation possible est de considérer les deux points P et Q liés à un plan mobile superposé au plan fixe de A et B ; ici, le plan mobile a un mouvement de rotation autour de C. |
 |
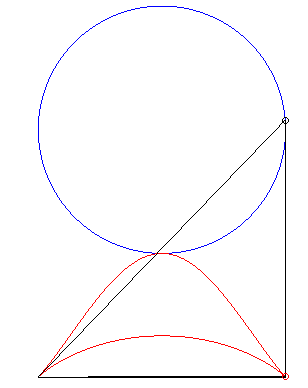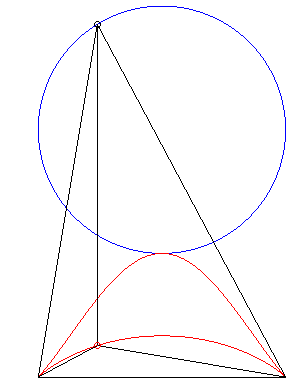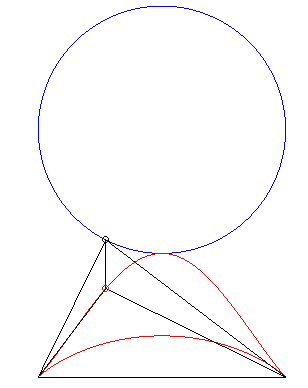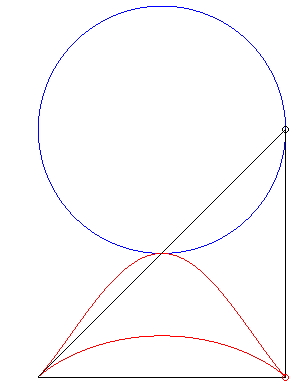
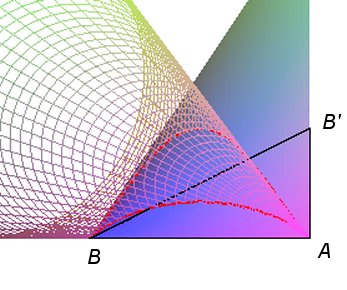
| Cette construction permet d'obtenir le bicorne par projection
orthogonale de l'intersection d'un cône elliptique avec un paraboloïde
hyperbolique (courbe biquadratique).
Le cône a pour sommet un point A1(a, 0, h) sur la verticale menée par A, et pour directrice le cercle (C). Le paraboloïde est défini par le quadrilatère gauche (A1B'BB1) où B'(a, a, 0) est le symétrique de B par rapport à C, et B1(–a, 0, h) est sur la verticale menée par B. |
 |
Autre caractérisation (Roland
Deaux, 1945) : le bicorne est le lieu du centre du cercle inscrit dans
un triangle dont deux sommets sont fixes et dont le périmètre
est égal à la somme des rayons des cercles exinscrits.
| Un point M d'un cercle se projette en P
et Q sur deux tangentes au cercle, perpendiculaires entre
elles ; lorque M décrit le cercle, la droite (PQ)
enveloppe une quartique ayant deux points de rebroussement, paramétrée
à similitude près par Mais ce n'est pas un bicorne car les tangentes aux points de rebroussement ne passent pas par le sommet. |
 |
|
|
|
 |
© Service audiovisuel École Polytechnique |
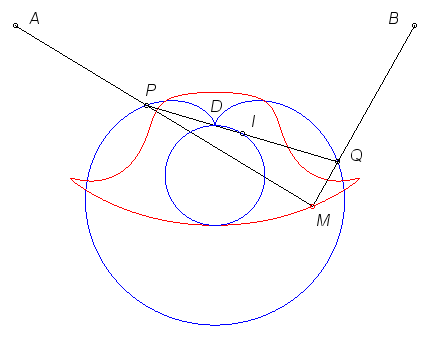
| ... Henri Lazennec a repris la construction de Jérabek
en remplaçant le cercle par une cardioïde.
Il considère les points A(–4, 0), B(4, 0), C(0, –3), D(0, –2). Le segment [PQ] de longueur fixe 4, passant par D et dont le milieu I décrit le cercle de centre C et de rayon 1 a ses extrémités décrivant une cardioïde de pointe D. Lorsque [PQ] tourne sur la cardioïde, l'intersection M de (AP) et (BQ) décrit une courbe à l'allure de bicorne, avec des pointes retroussées. Paramétrisation : |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016