CASSINIENNE
Cassinian
curve, Cassinische Kurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CASSINIENNE
Cassinian
curve, Cassinische Kurve

| Courbe étudiée par Serret
en 1843.
Dominique Cassini (1748-1845) : astronome français. Autres noms : courbe isodynamique, lemniscate. |
| Équation multipolaire : Équation complexe : Courbe algébrique de degré 2n, n-circulaire. Les cassiniennes et les stelloïdes sont les images réciproques des lignes de coordonnées par la fonction complexe f définie par Dans le cas d'un polygone régulier : Équation polaire : Équation cartésienne dans ce cas : |
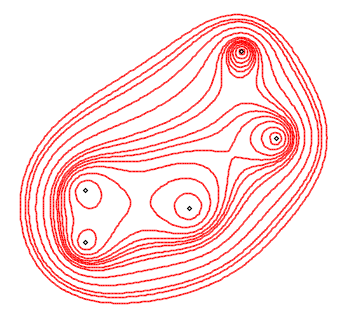
Les cassiniennes à n foyers
(ou n pôles) sont les lieux des points du plan dont la moyenne
géométrique des distances à
n points est constante.
Le cas n = 2 donne les ovales
de Cassini.
Les lignes de champ du champ magnétique créé par n fils parallèles parcourus par un courant de même intensité et de même sens sont, dans chaque plan orthogonal aux fils, les cassiniennes de foyers les points d'intersection avec les fils ; idem pour les équipotentielles du champ électrostatique créé par n fils parallèles uniformément chargés avec des charges identiques.
je cherche une photo de cette expérience avec de la limaille de fer !
On démontre que toute courbe fermée simple peut être approchée aussi près qu'on veut par une cassinienne, mais avec un nombre de pôles qui peut être très grand : théorème de la lemniscate de Hilbert (1897), voir plus de précisions ici.
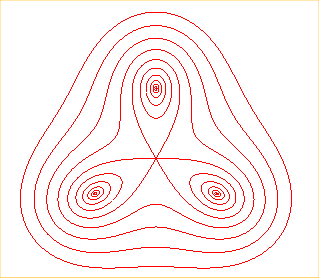
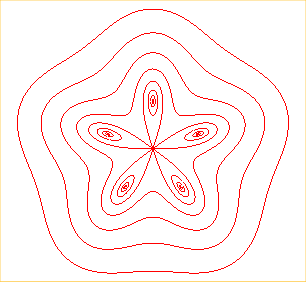
Lorsque les pôles sont les sommets d'un polygone régulier de centre O et de rayon a, Ox passant par l’un de ses sommets, on obtient l'équation polaire donnée ci-dessus.
Lorsque b < a, on obtient alors une courbe formée de n ovales entourant chaque sommet du polygone.
Lorsque b = a (i. e. lorsque la courbe passe par O), on obtient une spirale sinusoïdale de paramètre n.
Lorsque b > a, on obtient une courbe fermée
simple.
|
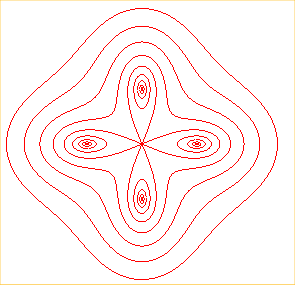
n = 4 |
|
Les trajectoires orthogonales de ces courbes quand b
varie sont des spirales
sinusoïdales de paramètre -n, toutes semblables
entre elles, d'équation polaire .
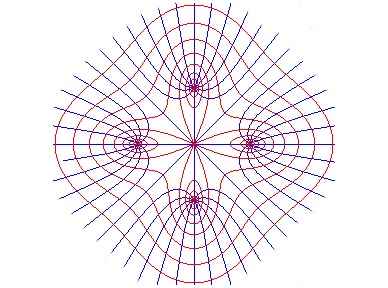
On peut généraliser les cassiniennes à
des moyennes géométriques pondérées, autrement
dit, pour une équation multipolaire du type :
; ces courbes s'obtiennent physiquement comme lignes de champ magnétiques
avec des fils parcourus par des courants des distincts, ou comme équipotentielles
électrostatiques avec des fils ayant des charges distinctes.
Par exemple, pour n = 2 et ,
on obtient un faisceau de
cercles
à points limites les pôles.
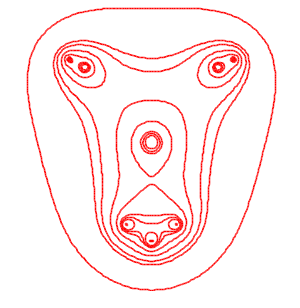
Des cassiniennes alien ... par Alain Esculier.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2005