Équation polaire de :   avec n réel. Équation complexe : . Equation différentielle polaire : . Abscisse curviligne obtenue par :  ou . Angle tangentiel polaire : . Équation podaire :  . Courbe algébrique si et seulement si n est rationnel. Dans le cas où n est entier positif : Équation multipolaire : , où  est un n-gone régulier de rayon a. Équation complexe : . Dans le cas où n = – m est un entier négatif : Équation multipolaire :  où  est un m-gone régulier de rayon a. Équation complexe : . Longueur :  ; aire : .

Les spirales sinusoïdales sont définies par leur équation polaire ci-dessus.
Lorsque n est un entier positif, les spirales sinusoïdales sont les lieux des points dont la moyenne géométrique des distances aux sommets d'un polygone régulier est égale au rayon de ce polygone ; ce sont donc des cas particuliers de cassiniennes à n pôles.

Lorsque n est un entier négatif, les spirales sinusoïdales sont les lieux des points M tels que la moyenne des angles des droites joignant les sommets d'un polygone régulier à M avec une direction fixe est constante ; ce sont donc des cas particuliers de stelloïdes.

et  sont inverses l'une de l'autre et la podaire de  est .
La construction de la tangente se fait simplement à partir de la relation :  .
Pour n > 0, la courbe est formée d'un motif de base symétrique par rapport à Ox obtenu pour :transformé par toutes les rotations d'angle  pour k entier ; pour n < 0, le motif de base est à asymptotes.

Lorsque n est rationnel, on obtient toute la courbe en effectuant les p – 1 rotations du motif de base pour  où p est le numérateur de n.
 

Exemples pour n positif :

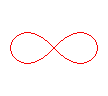
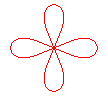
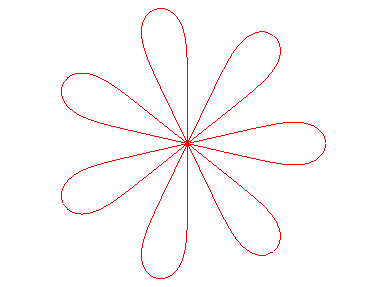
n = 1 : cercle	n  = 2 : lemniscate de Bernoulli	n = 3 : courbe de Kiepert.	n = 4	n = 5
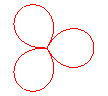
n = 1/2 : cardioïde	n = 3/2	n = 5/2	n = 7/2	n = 9/2
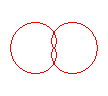
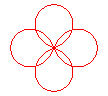
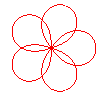
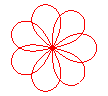
n  = 1/3 : sextique de Cayley	n = 2/3	n = 4/3	n = 5/3	n = 7/3
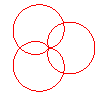
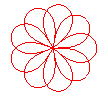
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
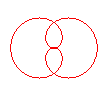
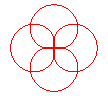
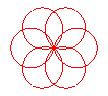
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Exemples pour n négatif :

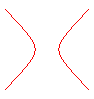
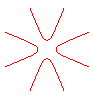
n = -1 : droite x = a	n  = -2 : hyperbole équilatère	n = -3 : cubique de Humbert	n = -4	n = -5
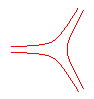
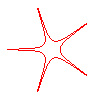
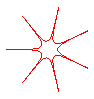
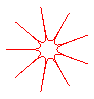
n =- 1/2 :  parabole y2 = 4a (a - x)	n = -3/2 Antipodaire centrale de courbe de Kiepert	n = -5/2	n = -7/2	n = -9/2
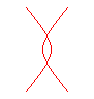
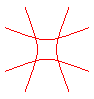
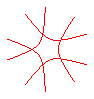
n  = -1/3 : cubique de Tschirnhausen	n = -2/3 antipodaire centrale de l'hyperbole équilatère	n = -4/3	n = -5/3	n = -7/3
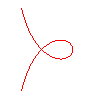
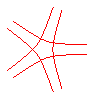
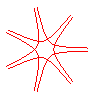
n = -1/4	n = -3/4	n = -5/4	n = -7/4	n = -9/4
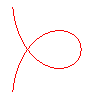
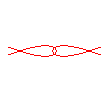
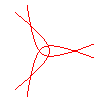
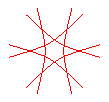
n = -1/5	n = -2/5	n = -3/5	n = -4/5	n = -6/5

Comparer avec les rosaces.
 
 

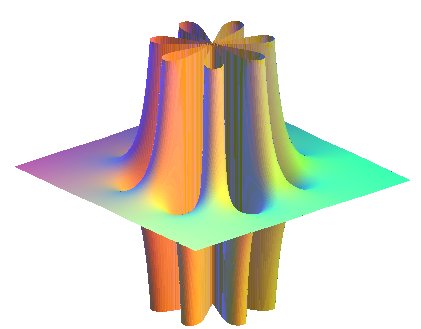
Les sections horizontales des deux surfaces associées à la fonction complexe , d'équations  sont des spirales sinusoïdales d'indice n. Ci-contre, le cas n = 7 et le cas  n = 4, gravure de Patrice Jeener.

La spirale sinusoïdale d'indice n est la ligne de champ du champ complexe (cf. la relation ) :

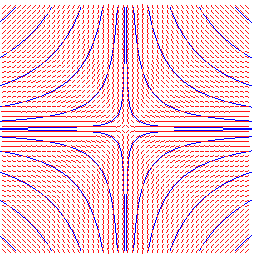
lignes de champ de 1/z : hyperboles d'indice -2	lignes de champ de Öz : paraboles d'indice -1/2	lignes de champ de z3/2  : cardioïdes d'indice 1/2
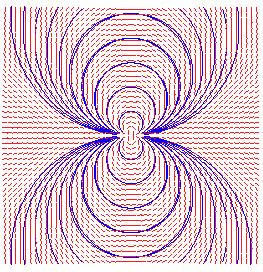
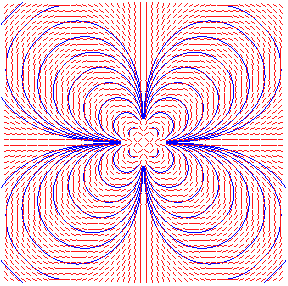
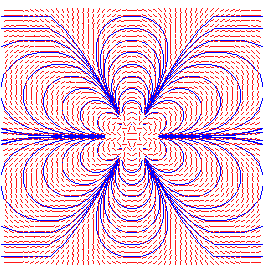
lignes de champ de z² : cercles d'indice 1	lignes de champ de z3 : lemniscates d'indice 2	lignes de champ de z4

Voir aussi l'exemple n°6 des trajectoires orthogonales.

La spirale sinusoïdale d'indice n est la trajectoire d'un point matériel de masse m attiré par une force centrale de norme   avec  , lancé en (a, 0) perpendiculairement à Ox avec une vitesse V₀ égale à   . Dans le cas normal de la gravitation ( = 2, soit n = – 1/2), on obtient la parabole, et la vitesse  V₀ est égale à la vitesse de libération (plus petite vitesse de départ pour laquelle le point matériel est envoyé à l'infini). Les cas  = 1 ou 3 (qui donneraient n = –1 ou 0) sont exclus ici ; pour le cas  = 3, voir à spirale hyperbolique, à épi, à spirale logarithmique et à spirale de Poinsot.

Les spirales sinusoïdales sont des projections planes des lignes asymptotiques des conoïdes de Plücker.

La roulette du pôle d'une spirale sinusoïdale d'indice n roulant sur une droite est une courbe de Ribaucour d'indice 1+1/n.

© Robert FERRÉOL 2018