Quadratrice de Dinostrate

QUADRATRICE DE DINOSTRATE
Dinostratus' (or Hippias') quadratrix, Quadratrix des Dinostratus (oder des Hippias)

Courbe étudiée par Hippias d'Elis en 430 avant J.C. et par Dinostrate en 350 avant J.C.
Dinostrate (IVe siècle avant J.C.) : mathématicien grec.
Autre nom : sectrice d'Hippias.

Paramétrisation cartéso-polaire :

.
Équation polaire :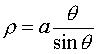

, où

.
Équation cartésienne :

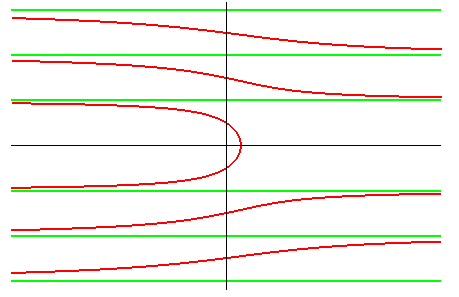La quadratrice de Dinostrate est le lieu des points d'intersection d'une droite en translation uniforme et d'une droite en rotation uniforme, les deux droites ayant une position commune ; à ce titre, c'est un cas limite de sectrice de Maclaurin, lorsque l'un des pôles se trouve à l'infini.
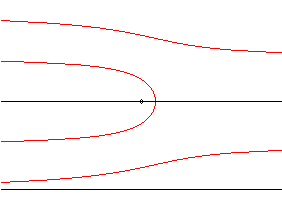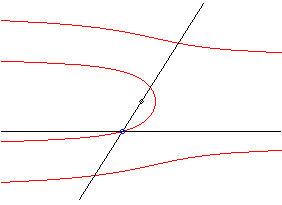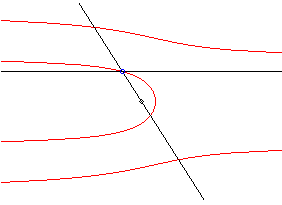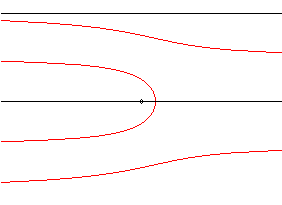C'est l'inverse par rapport à O d'une cochléoïde.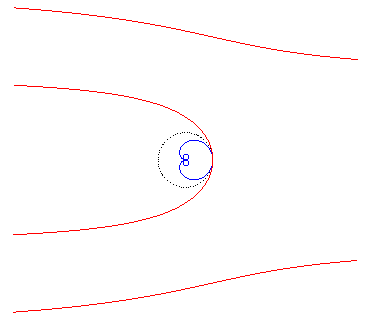
Si l'on considère la paramétrisation complexe , on a la propriété : ; toute suite définie par est donc tracée sur la quadratrice ; la limite de la suite est .

La quadratrice de Dinostrate est aussi la projection sur un plan perpendiculaire à l'axe de la section d'un hélicoïde droit par un plan contenant une génératrice de l'hélicoïde.

Comme son nom l'indique, cette courbe est une quadratrice ; en effet :.
Mais elle a tout d'abord été considérée par Hippias en tant que trisectrice et même n-sectrice ; en effet .
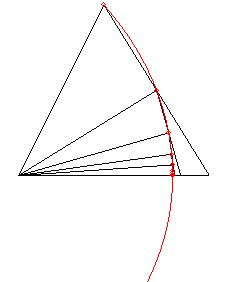
Si l'on étudie le cas général des lieux des points d'intersection d'une droite en translation uniforme et d'une droite en rotation uniforme, on obtient les courbes suivantes, qui sont aussi des multisectrices :

Paramétrisation cartéso-polaire : .
Équation polaire : 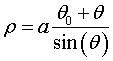, où .
Équation cartésienne : .
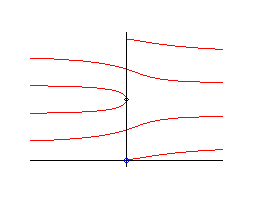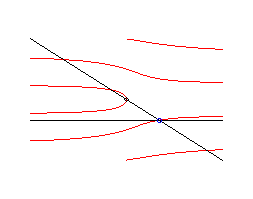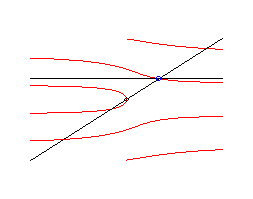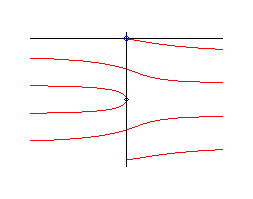
Cas où q₀ = p/2 , d'équation .

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres