COURBE DE GIRATION CONSTANTE
Curve
of constant gyration, Kurve aus konstanter Gyration
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE GIRATION CONSTANTE
Curve
of constant gyration, Kurve aus konstanter Gyration

| Courbe étudiée par moi-même suite
à une question de Franck
Rolland.
Animation ci-dessus réalisée par Alain Esculier. |
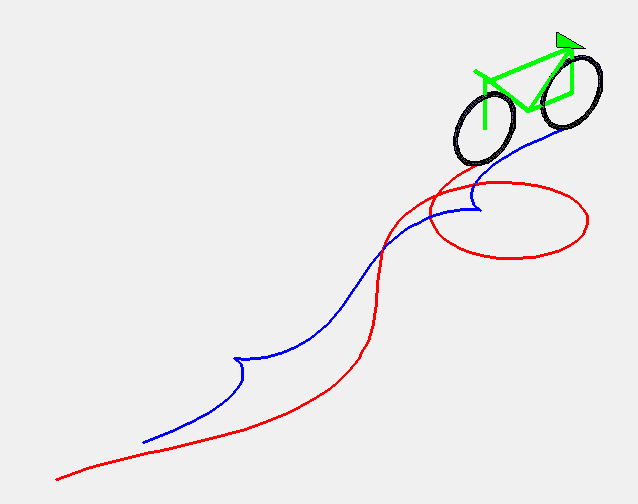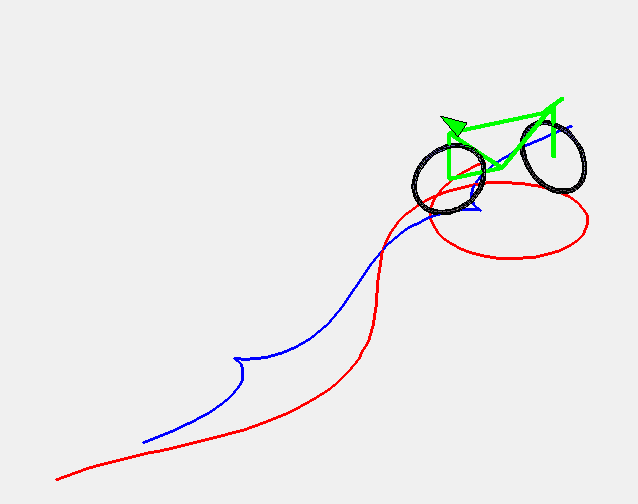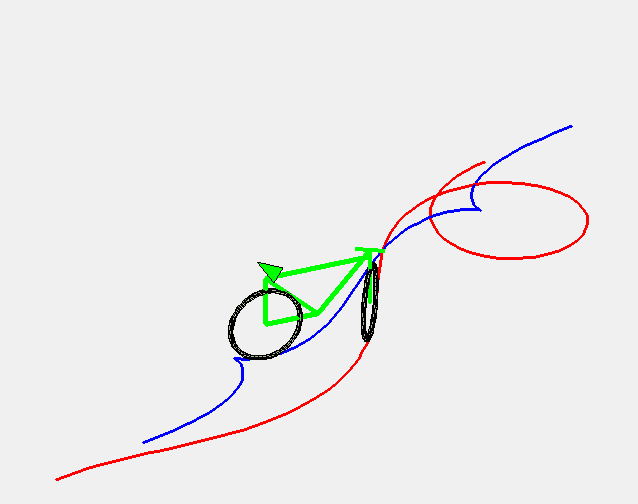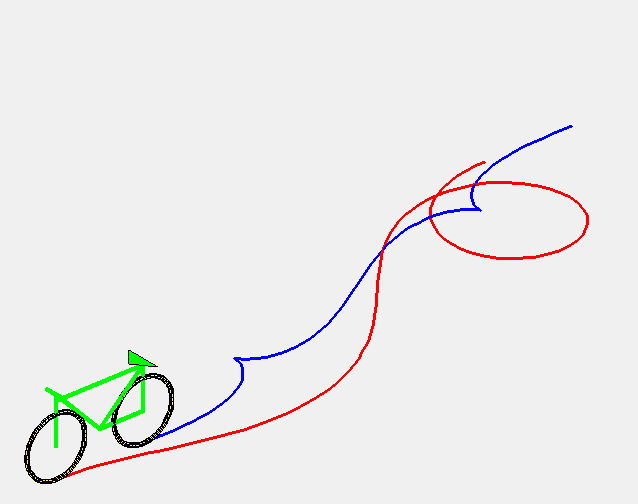
| 1) Courbe des roues avant :
Paramétrisation cartésienne : Abscisse curviligne : Équation intrinsèque 1 : 2) Courbe des roues arrière : |
La courbe de giration constante est la courbe décrite par les roues avant d'une voiture (mieux, d'un vélo) roulant à vitesse constante dont le conducteur tourne le volant à vitesse constante.
Plus précisément, c'est la courbe telle qu'une droite (D) passant par un point M de la courbe et faisant un angle avec la tangente proportionnel à l'abscisse curviligne ( (D) est l'axe de la voiture et le point M, les roues avant) reste tangente à une courbe en un point N (les roues arrières) situé à une distance constante de M.
C'est donc aussi la courbe dont la tractoire est telle que la laisse fait un angle avec la tangente qui est proportionnel à l'abscisse curviligne.
Voici quelques animations du mouvement pour une rotation complète du volant, avec une vitesse de rotation croissante.
k = 0,1 |

k = 0,2 |

k = 0,3 |

k = 0,4 |

k = 1 |
k = 5 |
On peut remarquer que si la courbe des roues avant se
reproduit à l'identique après que le volant ait fait un tour
complet, celle des roues arrière se reproduit seulement après
un demi-tour.
| Evolution de la courbe sur deux périodes pour
k
croisant de 0,1 à 1 puis ci-desous de 1 à 5 (vitesse de rotation
du volant croissante).
On remarquera un sorte de déroulement de la clothoïde jusqu'à devenir une sorte de cycloïde allongée.  |
 |
| Pour k tendant vers 0, la courbe de giration constante
s'identifie à la clothoïde
:
|
La courbe est fermée pour les valeurs de k telles que 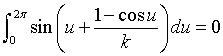 ),
comme par exemple k = 0,261 ci-dessous : ),
comme par exemple k = 0,261 ci-dessous :
 |
Démonstration de l'obtention de l'équation intrinsèque ci-dessus :
| Roues avant : Roues arrières : Rappels : La colinéarité de la vitesse des roues arrière avec Soit |
On peut généraliser le problème au cas d'une loi de variation de l'angle de braquage quelconque ; voici par exemple une animation du cas d'une loi sinusoïdale :

Comparer avec la courbe
à rayon sinusoïdal, pour laquelle le rayon de courbure
varie sinusoïdalement en fonction de l'abscisse curviligne (alors
qu'ici, c'est la courbure qui varie sinusoïdalement).
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2008