| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SPIRALE D'OR, SPIRALE DE FIBONACCI
et spirales naturelles
Golden
spiral, Fibonacci's spiral, goldene Spirale, Fibonaccische Spirale
|
|
|
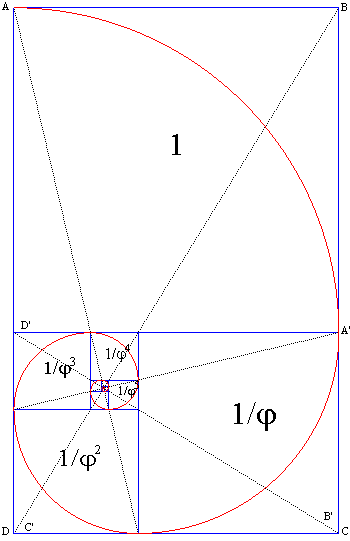
La figure est construite à partir d'un rectangle
d'or ABCD, avec AB = 1 et 
= le nombre d'or
; on trace le carré ABA'D' et on obtient un rectangle d'or
A'B'C'D'
de côtés 
et 1.
On réitère l'opération pour obtenir un rectangle A''B''C''D'' et ainsi de suite, et de même avec des carrés extérieurs ; la spirale d'or est formée de quarts de cercles successifs inscrits dans chaque carré. Les diagonales en pointillé BD et CD' se coupent au même point O qui est le point asymptote de la spirale, appelé "oeil de Dieu" (le nombre d'or étant aussi "la divine proportion" !) Les droites AA" et A'A''' sont orthogonales et se coupent en O. |
 |
La spirale d'or possède une propriété
"eadem mutata resurgo" partielle, à savoir qu'elle est invariante
par la similitude de centre O, de rapport 
et d'angle 
;
elle approche donc une vraie spirale logarithmique avec m défini par  ,
donc
d'équation polaire 
laquelle passe par les points A, A', A" etc...
A chaque tour le rayon
de la spirale d'or est multiplié par
|
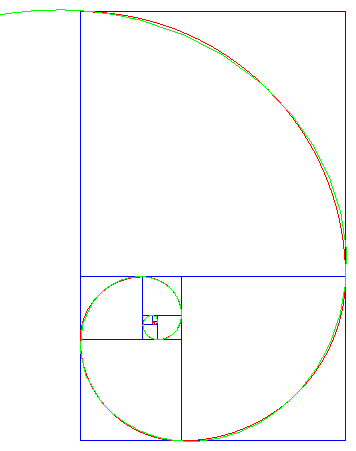
La spirale d'or (en rouge) et la vraie spirale logarithmique (en vert) |
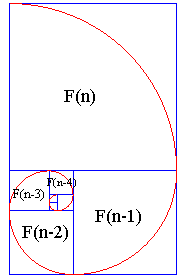
| Si, au lieu de partir d'un rectangle d'or, on part d'un
rectangle de Fibonacci, avec AB = Fn-1
et BC = Fn, où
Fn-1
et Fn sont deux nombres
de Fibonacci consécutifs, on obtient une spirale dite de Fibonacci
formée
de quarts de cercles. Elle approche la spirale d'or, mais ne possède
pas la propriété "eadem mutata resurgo".
Noter que cette construction utlise la propriété |
 |
 |
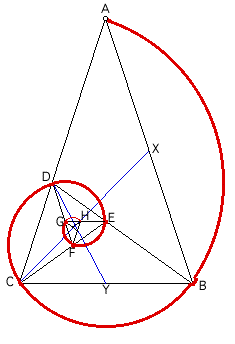
On peut aussi partir du triangle d'or (isocèle
d'angle au sommet  )
; on obtient alors une spirale que l'on peut appeler spirale d'or triangulaire
; cette spirale tournée de 
est agrandie dans un rapport ;
elle approche donc la spirale logarithmique 
; le coefficient d'agrandissement à chaque tour est de 
et l'angle tangentiel polaire est d'environ 76°. |
 |
| Voir aussi la spirale de Padovan, dont le coefficient d'agrandissement à chaque tour est la puissance sixième du nombre de Padovan soit environ 5,4. |
 |
| On trouve sur ce site une justification du fait que la coquille des nautiles approcherait une spirale d'or, mais ceci est manifestement contredit par une vue directe : la spirale du nautile est nettement plus resserrée et des mesures expérimentales montrent que son coefficient d'agrandissement par tour est d'environ 3 ce qui est nettement inférieur au 6,9 de la spirale d'or... |  |
 Ammonite : coefficient d'agrandissement nettement moindre.... |
La vrille du petit pois approcherait la spirale d'or triangulaire... |
 |
Comparer la construction de la spirale d'or à celle
de la spirale à
n centres, qui approche, elle, une spirale d'Archimède.
Timbre suisse de 1987
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2024
; l'angle tangentiel polaire constant est 
de la suite de Fibonacci.