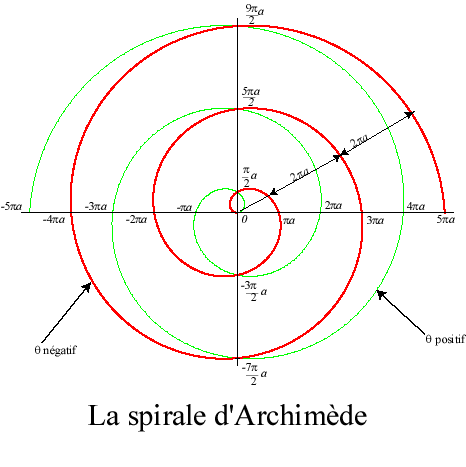Pour une spirale de pas  : Équation polaire : . Courbe transcendante. Caractérisation :  ( = angle tangentiel polaire). Abscisse curviligne : . Rayon de courbure : . Longueur de la n-ième spire obtenue pour  :   où  est la moyenne des longueurs des cercles de rayons ne et (n +1)e. Aire balayée par le rayon vecteur pour  : , de sorte que : .
	Par exemple, , ce qu'Archimède connaissait déjà : "La surface du premier tour de spirale est égale à un tiers de la surface du cercle dont le rayon est la longueur parcourue par le point sur la droite pendant le premier tour".

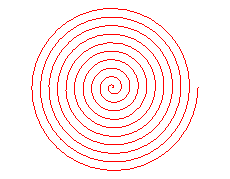
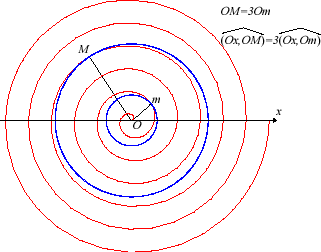
La spirale d'Archimède est la trajectoire d'un point se déplaçant uniformément sur une droite d’un plan, cette droite tournant elle-même uniformément autour d'un de ses points (réalisée par exemple par le sillon d'un bon vieux disque vinyle) ; ici, O est le centre de rotation, pour .

Bien voir tout de suite la différence avec la spirale logarithmique.

Par exemple, une personne située sur un plateau tournant à vitesse constante et se dirigeant à vitesse constante vers ou depuis le centre, décrit dans le repère fixe une spirale d'Archimède (voir la courbe du nageur et voir aussi la développante de cercle pour le cas où la personne ne se dirige pas vers le centre). Inversement, si une personne lance un ballon vers ou depuis le centre, le ballon décrira dans le repère du plateau une spirale d'Archimède (approchée car l'attraction terrestre modifiera cette spirale). Ci-contre, le manège inertiel de la Cité des Sciences.

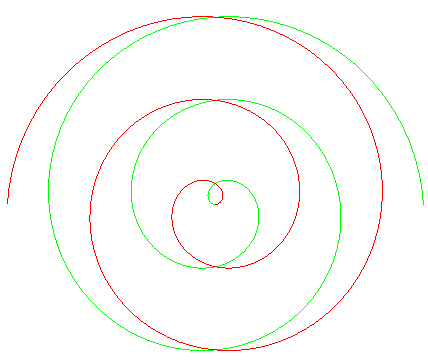
Une fois n'est pas coutume, la spirale complète , qui possède des points doubles, est nettement moins esthétique que la courbe ...	...qui n'en a pas, et partage le plan en deux régions connexes symétriques par rapport à O (cf. la spirale de Fermat)	C'est ainsi qu'a été lovée cette corde.

Remarque : toute conchoïde de cette spirale, d'équation , est encore une spirale d'Archimède, image de la précédente par une rotation d’angle –b/a. Ceci se traduit cinématiquement par le fait que si l'on fait tourner une spirale d'Archimède autour de son centre d'un mouvement uniforme, l'intersection de la spirale avec une droite passant par le centre décrit un mouvement uniforme (ceci sert à transformer un mouvement circulaire en mouvement rectiligne, par exemple pour le remplissage régulier d'une bobine de fil - cf. les anciennes machines à coudre ; voir aussi à développante de cercle).
Came en forme de coeur, formée de deux branches de spirales d'Archimède : le mouvement de rotation est transformé en la succession de deux mouvements rectilignes uniformes de sens contraires.	A droite de la machine à coudre, on distingue la came en forme de coeur.
Autre application : si un bâton de longueur 2a est astreint à coulisser au sommet d'une spirale d'Archimède, et son milieu à passer par la boucle centrale de cette spirale, les extrémités décrivent la came en forme de coeur précédente.

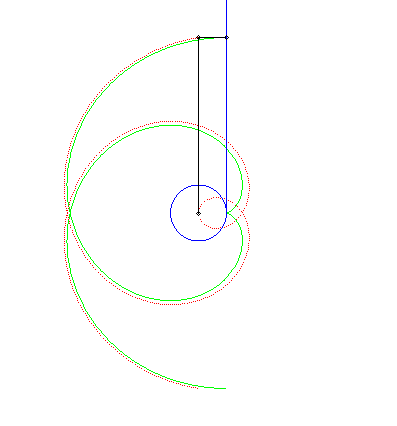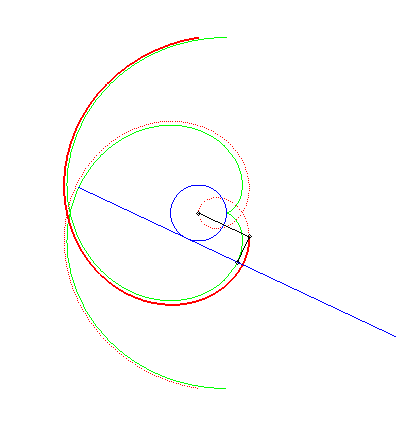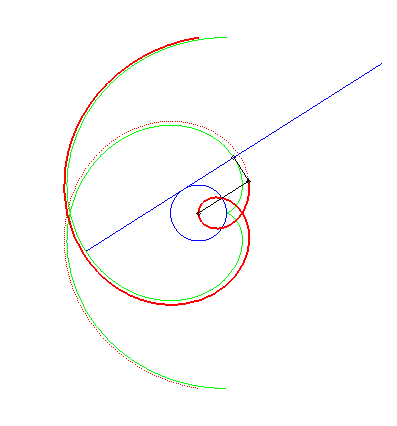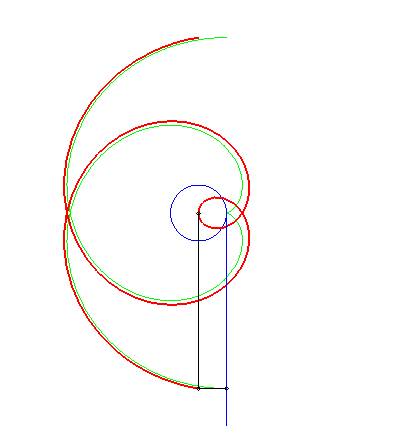
Théorème de Chasles : La spirale d'Archimède est la roulette obtenue en faisant rouler une droite sur un cercle de centre O et de rayon a et en prenant un point traceur situé à une distance à cette droite égale au rayon du cercle. Le projeté de ce point traceur sur la droite traçant, lui, une développante de cercle, on en déduit que la spirale d'Archimède est aussi la podaire de la développante de cercle. Cette développante de cercle, qui se construit donc très simplement en faisant rouler une droite sur un cercle est en fait un moyen simple de construire de manière aprochée la spirale d'Archimède.

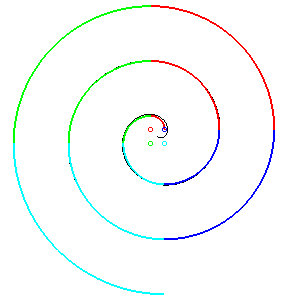
De même que la spirale d'or pour la spirale logarithmique, la spirale d'Archimède possède des constructions approchées par des arcs de cercles, comme la spirale à 4 centres ci-contre (les arcs de cercles sont colorés de la même couleur que les centres correspondants); cette construction se généralise à un nombre quelconque de centres.   Pb : la spirale d'Archimède noire (tangente en son centre à la diagonale du carré) est-elle asymptote à la spirale à 4 centres, comme le laisse suggérer cette figure ?

 

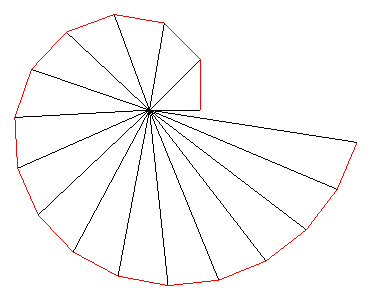
La spirale dite de Théodore (de Cyrène), ou escargot de Pythagore (en allemand, Quadratwurzelschnecke), fournit une construction approchée par des segments de droites d'une spirale d'Archimède. La construction des sommets 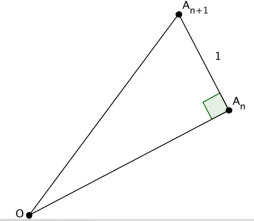de la ligne polygonale est indiquée ci-dessous, partant de  à distance 1 de O sur Ox. Le théorème de Pythagore montre alors que  , d'où l'intérêt de cette spirale. a pour angle polaire  et on montre que  et que  tend vers une constante = –2,15778...... La spirale de Théodore est donc asymptote à la spirale d'Archimède  comme on le voit bien sur la figure de droite (en rouge, Théodore, en bleu, Archimède).

La spirale d'archimède peut aussi être définie comme courbe à sous-normale polaire constante.
 

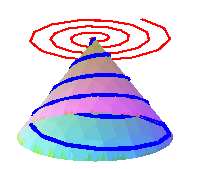
C'est enfin la projection (orthogonale) de la spirale conique de Pappus sur un plan orthogonal à l'axe du cône.

    - une quadratrice : si A est le point d'angle polaire  et B le point d'intersection de la tangente en A avec Oy, on a OB / OA = .

    - une trisectrice et même une n-sectrice : si une droite d'angle polaire  la coupe en, le cercle de centre O et de rayon la coupe en .
 
 

Voir à couple roue-route  le roulement d'une spirale d'Archimède sur une parabole.

Voir aussi la spirale conique de Pappus, analogue conique de la spirale d'Archimède, et la clélie, son analogue sphérique. Voir enfin la spirale Doppler.

Toute suite de points du plan complexe dont les modules et les arguments sont en progression arithmétique décrit une spirale d'Archimède.
 
 
 

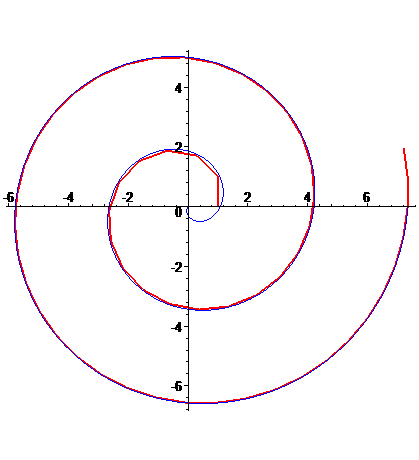
Par exemple, sur la figure ci-contre ont été tracés, pour n = 30, les points de coordonnées polaires , en bleu si l est pair, en rouge sinon ; ces points sont situés en quinconce à l'intersection de cercles concentriques de rayons en progression arithmétique et de droites concourantes ; mais ils sont aussi situés sur les spirales d'Archimède d'équation , d'où un joli effet.
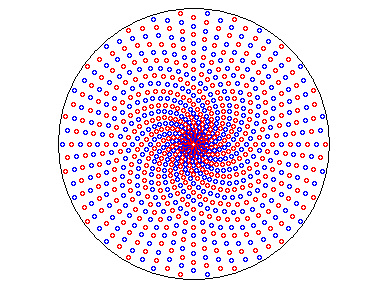Mosaiques en spirale de Guy Barthélémy.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2024