Triangle de Sierpinski

TRIANGLE DE SIERPINSKI
Sierpinski gasket, Sierpinski-Gasket

Fractal étudié par Sierpinski en 1915.
Autre nom : tamis de Sierpinski.
L'appellation "Sierpinski gasket" (soit "joint de culasse de Sierpinski"), est due à Mandelbrot.
Waclaw Sierpinski (1882-1969) : mathématicien polonais.
Voir la page d'Alain Esculier pour les programmes des figures de cette page.

Le triangle de Sierpinski est un fractal de Sierpinski dont l'objet de départ est un triangle plein :

C'est l'attracteur de 3 homothéties de rapport 1/2 centrées aux sommets d'un triangle équilatéral ; dimension fractale =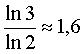

Le triangle de Sierpinski est aussi la limite d'une suite de courbes continues sans point double dites courbes du triangle de Sierpinski (en anglais : Sierpinski's arrowhead curves : courbes de Sierpinski en pointe de flèche) .

Le triangle de Sierpinski est en effet aussi l'attracteur des trois similitudes directes de rapport 1/2 transformant (A,B) en (P,A), (P,Q), et (B,Q) respectivement (où [PQ] est segment médiant d'un triangle équilatéral ABC).
C'est aussi l'attrcateur de trois similitudes, la première et la dernières indirectes, la deuxième directe, de raport 1/2, transformant (A,B) en (A,P), (P,Q), et (Q,B) respectivement
En partant du segment [AB], cela donne les courbes suivantes :
Code Maple, similitudes directes du premier cas:
t:=Pi/3:r:=1+2*cos(t):
sierpinski:= proc(A,B,n)
if n=0 then [A,B]:
else P,Q:=A+(B-A)*exp(I*t)/r,B-(B-A)*exp(-I*t)/r:
sierpinski(P,A,n-1),
sierpinski(P,Q,n-1),
sierpinski(B,Q,n-1) fi: end:
plot(map(X ->map(z ->[Re(z),Im(z)],X),[sierpinski(0,1,5)]),
axes=none,color=red,scaling=constrained);

Code Maple, similtudes du deuxième cas :
with(plots): t:=Pi/3:r:=1+2*cos(t):
sierpinski:=proc(n)
if n=0 then [1]
else L:=sierpinski(n-1):
L1:=map(z->conjugate(z)*exp(t*I)/r,L):
L2:=map(z->L1[-1]+z/r,L):
L3:=map(z->conjugate(z)*exp(-t*I)/r+L2[-1],L):
[op(L1),op(L2),op(L3)]: fi end:
complexplot([0,op(sierpinski(5))],scaling=constrained,axes=none);

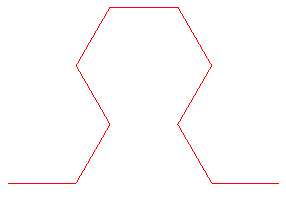
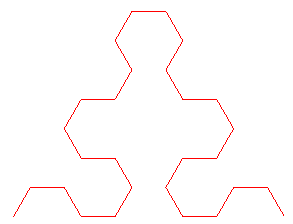
Le triangle de Sierpinski a un lien inattendu avec celui de Pascal, visualisé sur la figure ci-dessous :

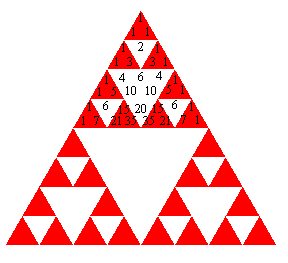
Les coefficients impairs sont sur les cases rouges et les pairs sur les blanches !

Sierpinski coke
Coquillage de Sierpinski
Si l'on n'effectue pas les retrournements, on obtient cette courbe ressemblant à la courbe du C.

fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres