Two families of curves are said to be orthogonal when at every point common to a curve of each family, the tangents are orthogonal, and one of the families is said to be composed of the orthogonal trajectories of the other. This constitutes a double orthogonal system of curves.
 

	If the first family of curves is defined by:	then the orthogonal trajectories are defined by:
Geometrical definition	f( M ) = constant	g (M) = constant with
Cartesian implicit equation	P(x, y) = constant	Q(x, y ) = constant with
Harmonic Cartesian implicit equation	P(x, y) = constant with P harmonic	Q(x, y ) = constant with
Complex implicit equation	Re (f (z) ) = constant with f holomorphic (hence conformal)	Im (f (z) ) = constant
Polar implicit equation	P(r, ) = constant	Q(r, ) = constant with
Cartesian differential equation	y' = f(x, y)	y' = -1 / f(x, y)
Polar differential equation	r' = f(r,)	r' = - r² / f(r, )
Field lines of the Cartesian field:	(f(x, y), g(x, y))	(g(x, y), -f(x, y))
Field lines of the polar field:	(f(r, ), g(r,))	(g(r, ), -f(r, ))

If both the families are given by a unique parametric form: , with fixed u and variable v for the first family, fixed v and variable u for the second one, then the families are orthogonal iff , which is always the case when P and Q are the real and imaginary part of a holomorphic function (inverse function of the one above).

The orthogonal trajectories of a family of lines are the involutes of the envelope of this family; therefore, they are parallel curves (see example 13 below).

Examples :

Definitions	Common parametric expression (red curves: u = constant blue curves: v = constant)	Inverse images of the Cartesian coordinate lines by the conformal map f defined by	Physical interpretation of the red curves	Plot
1 initial curves (red circles) orthogonal curves (blue lines) Cartesian polar implicit equation x² + y² = cte r = a differential equation yy' + x = 0 r' = 0 field (y, -x) (0 , 1) Cartesian polar implicit equation y = kx = q0 differential equation xy' - y = 0 d/dr = 0 field (x, y) (1 , 0)		so	Magnetic field lines induced by a uniform linear current orthogonal at O to xOy. Electrostatic equipotential induced by a charge placed at O or charges uniformly distributed on a line orthogonal at O to xOy
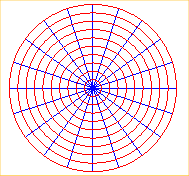2 Family of homofocal parabolas initial curves (red parabolas) orthogonal curves (blue parabolas) Cartesian polar implicit equation  y² = 4u²(u²-x) r=2u²/ (1+cosq) differential equation yy'²+2xy'-y=0 Cartesian polar implicit equation y² = 4v²(v²+x) r=-2v²/ (1+cos) differential equation yy'²-2xy'-y=0		so
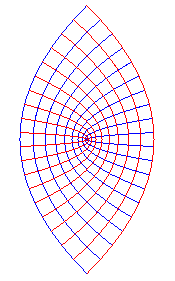3 initial curves (red hyperbolas) orthogonal curves (blue hyperbolas) Cartesian polar implicit equation x² - y² = cte r²cos2= cte differential equation yy' - x = 0 r' = r tan2 field (y, x) (sin2, cos2) Cartesian polar implicit equation xy = cte r²sin2= cte  differential equation xy' + y = 0 r' = -r cot2 field (-x, y) (-cos2 , sin2)		so	Approximate view of the example n° 8 below in a neighbourhood of O. They are the contour lines of the hyperbolic paraboloid
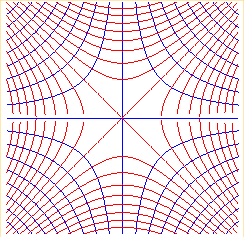4 initial curves (red circles) orthogonal curves (blue circles) Cartesian polar implicit equation x² + y² = ax r = acos differential equation 2xyy' =   y²-x² r' + r tan = 0 field (2xy,  y² - x²) (sin, -cos) Cartesian polar implicit equation (x² + y²) = ay r = asin differential equation  ( y² - x²) y' + 2xy = 0 r' = r cot field (x² - y², 2xy) (cos, sin)			limit case of the example n°7 below when the conductors are infinitely close. See also the Smith chart.	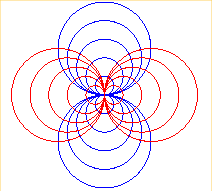= two pencils of orthogonal singular circles
5 initial curves (red cardioids) orthogonal curves (blue cardioids) polar implicit equation r=acos²/2 differential equation r' = r tan /2 field (sin/2, cos/2) polar implicit equation r=asin²/2 differential equation r' = -r cot/2 field (-cos/2 , sin/2)			Remark: figure obtained by inversion of that of the example n° 2.
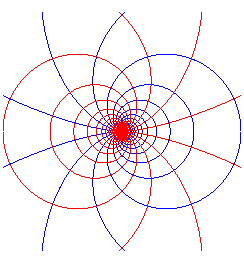6 initial curves (red sinusoidal spirals of index -n) orthogonal curves (blue sinusoidal spirals of index -n) polar implicit equation rncosn= cte differential equation r' = r tan n field (sinn, cosn) polar implicit equation rnsinn= cte  differential equation r' = -r cotn field (-cosn , sinn) The four previous cases correspond to n = 1/2, n = 2, n = -1 , n =-1/2		so	Opposite, view for n = 4 and n = -4.
7 initial curves (red double eggs) orthogonal curves (blue curves of the dipole) Cartesian polar implicit equation (x² + y²)3 = a²x4 r = acos² differential equation 3xyy' =  2 y²-x² r' + 2r tanq = 0 field (3xy, 2 y² - x²) (2sin, -cos) Cartesian polar implicit equation (x² + y²)3 = a4y² r² = a²sin differential equation  (2y²-x² ) y' + 3xy = 0 2r' = r cot field (x² - 2 y², 3xy) (cos, 2sin) Remark: the examples 4 and 7 are part of the more general example of Clairaut's curves: r = acosn and rn= ansin.	????	????	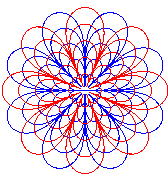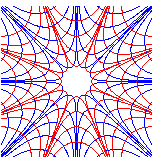Field lines of a magnetic dipole Field lines of an electrostatic dipole (limit case, inverting the red and blue curves, of the example 9 below).
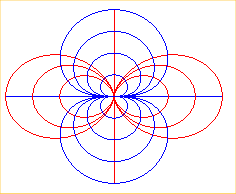8 initial curves (red circles) orthogonal curves (blue circles) geometrical definition MA/MB = constant with A(1,0) and B(-1,0) implicit equation (x - a)² + y² =  a² - 1 differential equation y' (x² - y² - 1) = 2xy geometrical definition (MA, MB) = constant implicit equation x² + (y - a)² =  a² + 1 differential equation 2xyy' = -x² + y² + 1 field MA/MA² - MB/MB²		so	Magnetic field lines induced by a uniform linear current orthogonal at A to xOy and a parallel current, in the opposite direction, passing by B. Electrostatic equipotential lines induced by charges uniformly distributed on a line orthogonal at A to xOy and opposite charges uniformly distributed on a line orthogonal at B to xOy.	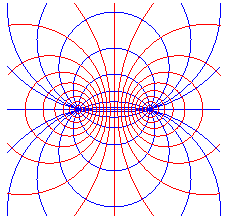= two pencils of orthogonal circles
9 initial curves (red Cassinian ovals) orthogonal curves (blue rectangular hyperbolas) geometrical definition MA .MB = constant   polar implicit equation r4 - 2r² cos2= cte differential equation r'( r2 - cos2) +rsin2=0 field (sin2, cos2 - r²) geometrical definition (Ox, AM) + (Ox, BM) = constant field MA/MA² - MB/MB² polar implicit equation r² = cos2a / cos(2(-a)) differential equation sin2r'= r3 - rcos2q field (r² - cos2, sin2)		so	Magnetic field lines induced by a uniform linear current orthogonal at A to xOy and a parallel current, in the same direction, passing by B. Electrostatic equipotential lines induced by charges uniformly distributed on a line orthogonal at A to xOy and equal charges uniformly distributed on a line orthogonal at B to xOy.	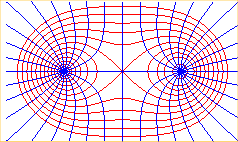See a generalisation at Cassinian curve for the red curves, and at stelloid for the blue curves: case where .
10 initial curves (red Cayley equipotential lines) orthogonal curves (in blue) geometrical definition 1/MA-1/MB = cte field geometrical definition field MA/MA3 - MB/MB3			Electrostatic equipotential lines induced by two opposite charges placed at A and B, in other words, an electrostatic dipole.
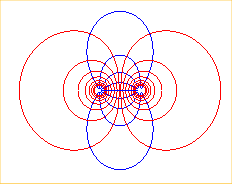11 initial curves (red Cayley ovals) orthogonal curves (in blue) geometrical definition 1/MA + 1/MB = constant field geometrical definition field MA/MA3 + MB/MB3			Electrostatic equipotential lines induced by two equal charges placed at A and B.
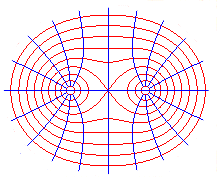12 Lattice of homofocal conics initial curves (red ellipses) orthogonal curves (blue hyperbolas) geometrical definition MA + MB = constant field MA/MA - MB/MB Cartesian equation x²/(1+cte)+y²/cte=1 geometrical definition MA - MB  = constant field MA/MA + MB/MB Cartesian equation x²/(1-cte)-y²/cte=1		f(z) = argcosh(z) f-1(z) =  cosh (z) (image of the first lattice by the Joukovski transformation: j(z) = (z + 1/z)/2)	Electrostatic equipotential lines induced by charges uniformly distributed on the segment line [AB]??? Interference pattern
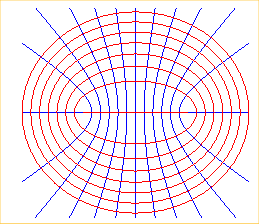13 Involute of circles and their generatrices initial curves (red half-involutes of a fixed circle) orthogonal curves (blue half-tangents to the circle) complex parametrization complex parametrization	????	????
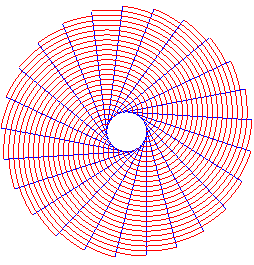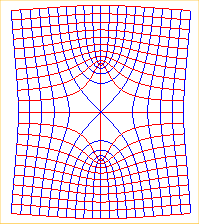
14 initial curves (red quartics) orthogonal curves (blue quartics) Cartesian implicit equation  y² = a²(1  + 1 / (a²+x²)) parametrization x = a tan t y² = a²  + cos²t Cartesian implicit equation x² = a²(1 - 1 / (a²+y²)) parametrization  x² = a²  - cos²t y = a tan t			Streamlines of a uniform flow perturbed by an obstacle (the segment line [AB] with A(0, 1) and B(0, -1))	The blue curve passing by O (obtained for a = 1) is a bullet nose curve
15 initial curves (red cubic hyperbolas) orthogonal curves (blue cubic hyperbolas) Cartesian implicit equation (y - constant) (x²+y²) = y Cartesian implicit equation (x - constant) (x²+y²) + x =0		where j is the Joukovski transformation	Streamlines of a uniform flow perturbed by the disk with centre O and radius 1.
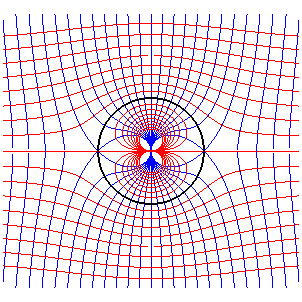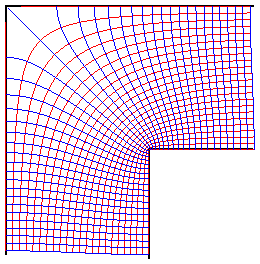
16 where . For example, when v = pi/2, we get:			Streamlines of a uniform flow in a bent tube.

Other examples:
 

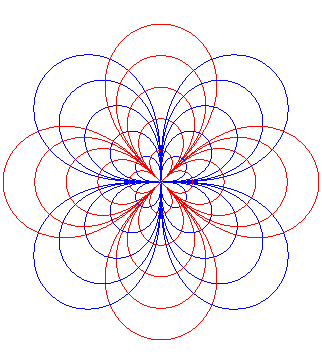
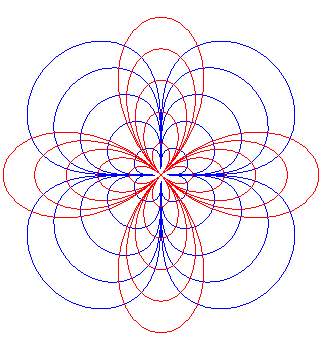
Lemniscates of Bernoulli : and  (case n = –2 of the example 6 above)	Quatrefoils ; and their orthogonal trajectories .
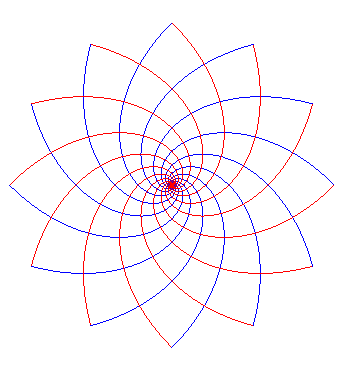
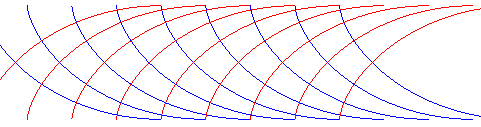
Logarithmic spirals: and.	Parabolas  and ellipses
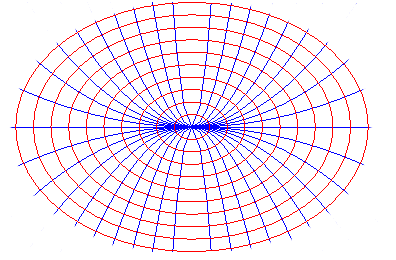Red parabolas  and semicubical parabolas .	cycloids: and symmetric cycloids

See also tractrix, as well as this article.

The projection on a horizontal plane of the slope and contour lines of a surface form two orthogonal lattices; see for example the egg box.

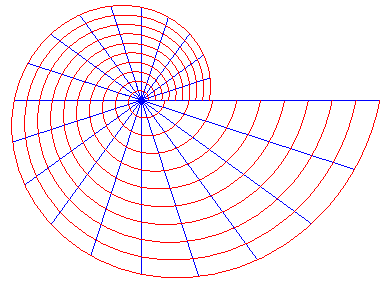
This notion of orthogonal curves can be generalised to any angle; two families of curves intersect under the angle V when, at each point common to the families, the tangents form an angle V, and one of the families is composed of the trajectories at angle V of the other one.

For example, the trajectories under the angle V of the pencil of lines passing by O are the logarithmic spirals;:

The 3D generalisation of the double orthogonal systems is the notion of triple orthogonal system of surfaces.
 
 

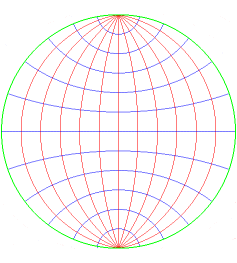
Map obtained by stereographic projection with the pole a point on the equator; the parallels and the meridians form two bundles of orthogonal circles. Bourse du commerce, Paris.

 
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2022