CYCLOÏDE
Cycloid,
Zykloide

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CYCLOÏDE
Cycloid,
Zykloide


| Courbe étudiée par Charles Bouvelles en
1501, Mersenne et Galilée en 1599, Roberval en 1634, Toricelli en
1644 etc...! Cette courbe n'était donc pas connue des Grecs.
Du grec kuklos : cercle, roue ; nom donné par Galilée. |
| Paramétrisation cartésienne : Autre paramétrisation : Paramétrisation complexe : Équation cartésienne : Équation différentielle : Est également solution de Abscisse curviligne : 1) Angle tangentiel cartésien : 1) 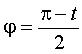 .
.
Rayon de courbure : 1) Équation intrinsèque 1 (forme 1)): Équation intrinsèque 2 (forme 1)) : Longueur d'une arche : 8R Aire délimitée par une arche et la base : 3 Barycentre de l'arche-courbe : Gc = ( Barycentre de l'arche-domaine : Gd = ( Hauteur moyenne : |
 |
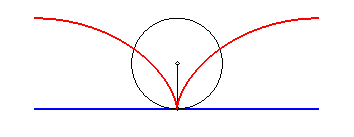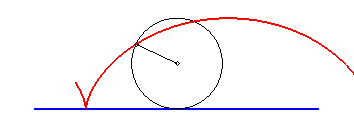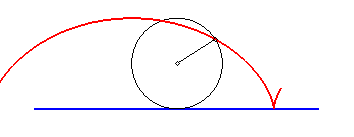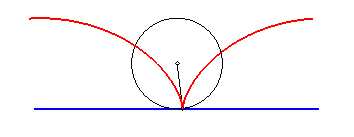
La cycloïde est la courbe décrite par un point d'un cercle de rayon R roulant sans glisser sur une droite (D) (ici l’axe Ox) ; c’est donc un cas particulier de roulette.
On peut aussi définir la cycloïde comme la
trajectoire d’un mouvement composé d’un mouvement rectiligne uniforme
et d’un mouvement circulaire uniforme de même vitesse (de paramétrisation
complexe : ) ; autrement
dit, si vous avancez régulièrement le long d’un tableau tenant
une craie à la main d’un mouvement circulaire régulier de
même vitesse que votre mouvement propre (d’un sens ou d’un autre),
vous tracez une cycloïde (sans la condition d’égalité
des vitesses, on obtient une trochoïde).

La cycloïde est un cas particulier de courbe
cycloïdale, avec les épicycloïdes
et les hypocycloïdes
; c'est aussi une courbe de Ribaucour.
| La cycloïde peut aussi être définie par le fait qu'étant donné deux droites parallèles, les deux points I et N d'intersection de la tangente et de la normale avec ces deux droites sont tels que la droite (IN) reste orthogonale à ces deux droites. | 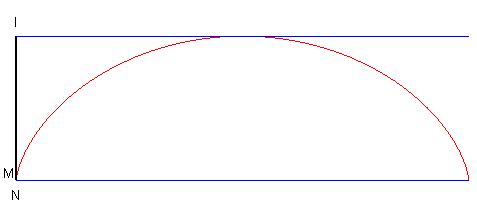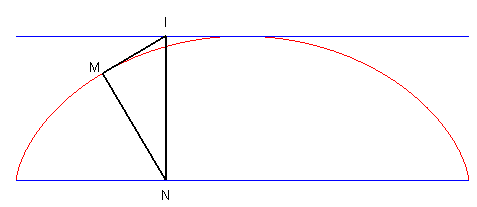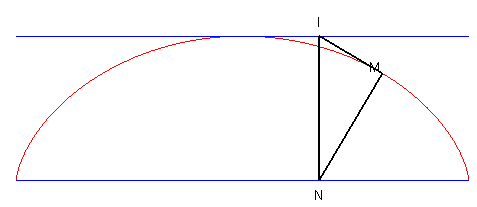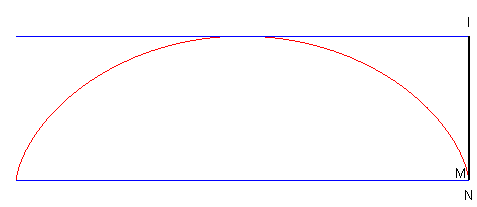 |
La développée de la cycloïde est une cycloïde translatée :
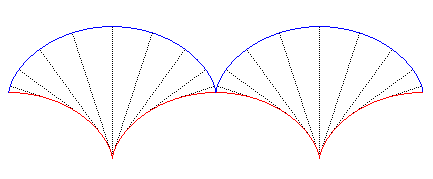
La développante
d'une cycloïde passant par l'un des sommets est donc aussi une cycloïde
translatée.
| La cycloïde est donc en quelque sorte un point fixe de l'application développante, et l'on a le théorème de « convergence » associé ci-contre : | Si on part d'un arc compact D0 de classe C2 sans point d'inflexion et dont les tangentes aux extrémités A = A0 et B = B0 sont orthogonales, sa développante D1 qui passe par A aura les mêmes propriétés : soit A1= A et B1 ses extrémités. On considère la développante D2 de D1 qui passe par B1, et on continue le processus. On ramène toutes les courbes Dnobtenues dans un même rectangle par des translations adéquates de direction la tangente en B à D, de façon que D2n+1 ait A pour origine et que D2n ait B pour origine. Alors D2n+1 et D2n tendent uniformément vers deux demi-arches de cycloïde droite. |
| La développante passant par le point de rebroussement
est, elle, la courbe (parallèle à une cycloïde) de paramétrisation
: Il se trouve que c'est aussi, à homothétie près, la roulette du point de rebroussement d'une cardioïde roulant sur et à l'extérieur d'une cycloïde de même longeur ! (Si la cardioïde roule à l'intérieur, la roulette est rectiligne) |
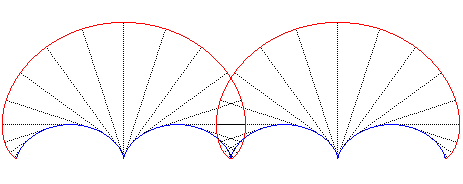 |
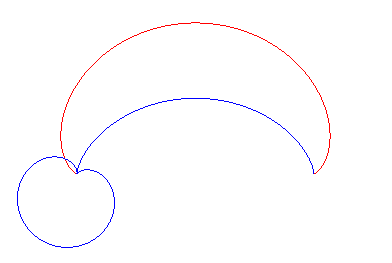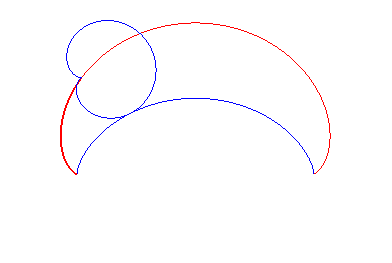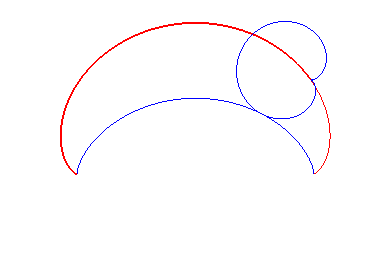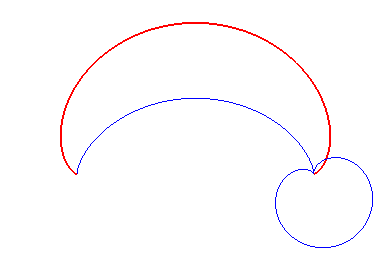 |
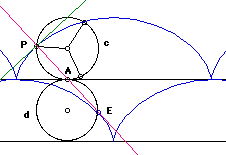
| Le diamètre du cercle traceur enveloppe une autre cycloïde, qui est l'image de la cycloïde de départ dans une homothétie de rapport 1/2. Il se trouve que la caustique au soleil pour des rayons perpendiculaires à l'axe de roulement est cette même cycloïde. | 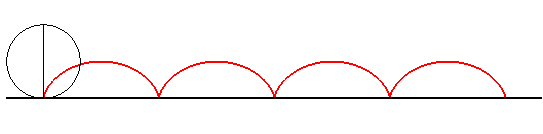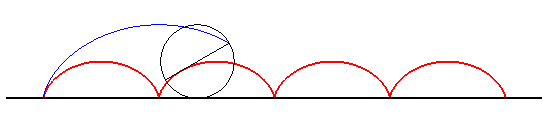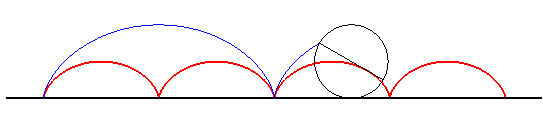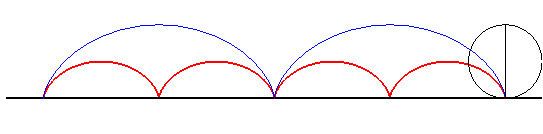 |
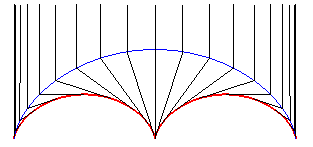 |
| La radiale de la cycloïde est un cercle de rayon 2R : |
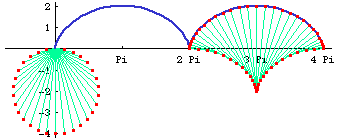 |
| Sa courbe de Mannheim
est également un cercle, de rayon 4R (cf. l'équation intrinsèque
1) ; c'est cette propriété qui est sous-jacente à
cette étrange courbure d'un disque en coquille Saint Jacques. Lorsque
la courbe verte atteint sa courbure maximale, elle est une arche de cycloïde,
ainsi que la courbe rouge supérieure, qui est sa développée.
Animation due à Gérard Lavau sur une idée de Samuel Boureau. |
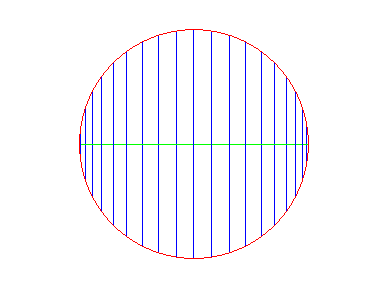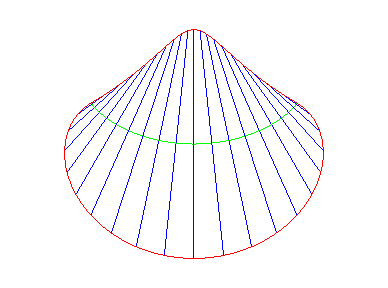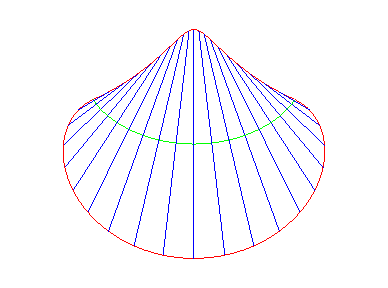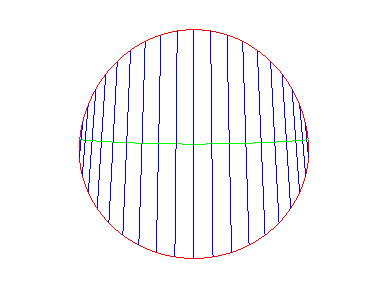 |
Démonstration de ce fait, par Gérard Lavau :
Considérons un disque visualisé sous forme d'un diamètre et d'un certain nombre de cordes orthogonales à ce diamètre. Le diamètre est considéré comme flexible, les cordes restant perpendiculaire à celui-ci ; on courbe ce diamètre au maximum, sans que les cordes ne se chevauchent. Cela impose que le rayon de courbure de la courbe finale suivie par le diamètre déformé soit en tout point égale à la demi-longueur de la corde en ce point. Supposons que le diamètre soit initialement défini par y = 0 et |
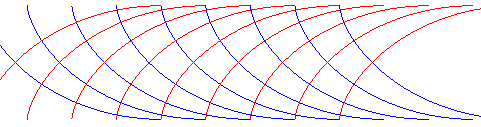
La roulette de la pointe d'une cardioïde roulant sur une cycloïde de même longueur est rectiligne :

Voir d'autres propriétés remarquables de la cycloïde à brachistochrone, tautochrone, isochrone, caustique et radiale.
La rotation d'une cycloïde autour de sa base donne une surface dont la courbure parallèle est le double de la courbure méridienne en tout point.
Voir aussi la surface minimale de Catalan, seule surface minimale ayant la cycloïde comme géodésique.
Généralisations : trochoïde,
cycloïde
elliptique.
|
|
 |
 |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2022