Deux courbes  et  forment un couple roue-route si l'on peut faire rouler sans glisser  sur  de sorte qu'un point fixe du plan de  (le moyeu de la roue) ait une trajectoire rectiligne dans le plan fixe. Il s'agit donc d'un mouvement plan sur plan dont la base est , la roulante  et dont une roulette est rectiligne.
Les courbes  et  peuvent aussi être considérées comme deux profils conjugués d'engrenages, le moyeu de  étant situé à l'infini (considérer le mouvement dans un repère lié au moyeu de la roue).
 

Si la roue  est donnée par son équation polaire, le moyeu étant situé en O, et la route  par son équation cartésienne, les formules reliant les deux équations sont . Partant d'une roue , on obtient la route  où F est une primitive de fg' (transformation de Grégory). Partant inversement d'une route , on obtient la roue  où H est une primitive de . Si la roue est donnée par son équation podaire : , l'équation différentielle de la route est .

Cette notion a été initialement étudiée non pour une utilisation pratique de roues non circulaires, mais parce que les calculs de l'abscisse curviligne sont les mêmes pour les deux courbes (pour la route, en coordonnées cartésiennes, et pour la roue, en coordonnées polaires) et que donc la rectification de l'une donne celle de l'autre.
Il existe 2 théorèmes fournissant une définition géométrique de la route à partir de la roue.
 

1) Théorème de Steiner-Habich  : la route est la roulette à base rectiligne de l'antipodaire de la roue ; plus précisément, si l'on fait rouler l'antipodaire  de la roue par rapport au moyeu sur une droite, le lieu du moyeu est la route. Autrement dit : étant donné une courbe  et un point, la podaire de cette courbe par rapport au point et sa roulette à base rectiligne forment un couple roue-route.

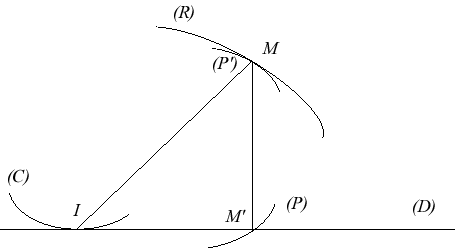
Lorsque (C) roule sur (D), un point M du plan de (C) décrit une roulette (R) dans le plan fixe. La podaire (P) de (C) par rapport à M coupe (D) au projeté M' de M sur (D) ; on montre alors que la courbe (P') symétrique de (P) par rapport à la médiatrice de [MM'] roule sans glisser sur la courbe (R), ce qui établit le théorème de Habich, puisque M' décrit (D).

2) Théorème de Mannheim :
Etant donné une courbe  et un point, la radiale de cette courbe par rapport au point et sa courbe de Mannheim forment un couple roue-route.

Exemples :

Si la roue est circulaire avec un moyeu centré, la route est une droite parallèle à la trajectoire du moyeu et c'est le seul cas où ceci ce produit, mais il n'y a pas que ce cas bien connu !
 

Avec une roue circulaire, mais un moyeu situé sur le bord, la route est circulaire ; on retrouve le dispositif de La Hire. La courbe  est une cycloïde.
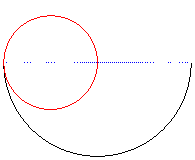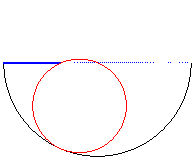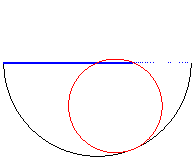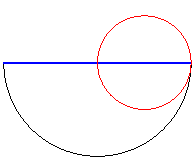Avec une roue circulaire et un moyeu quelconque, la courbe  est alors une ellipse ou une hyperbole suivant que le moyeu est interne ou non au cercle, avec le moyeu en un foyer ; la route est alors une roulette de Delaunay.
Si la roue est rectiligne (= cercle de rayon infini), la courbe  est une parabole avec le moyeu au foyer ; la route est une roulette parabolique de Delaunay, autrement dit une chaînette :. La courbe  est une chaînette d'égale résistance.
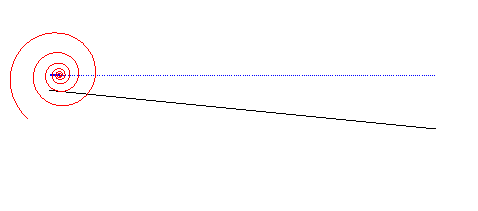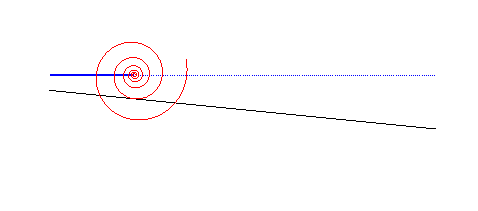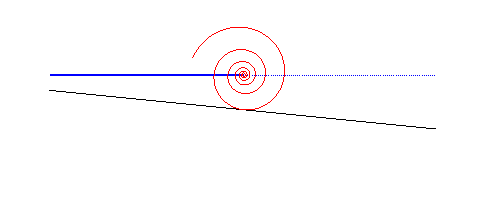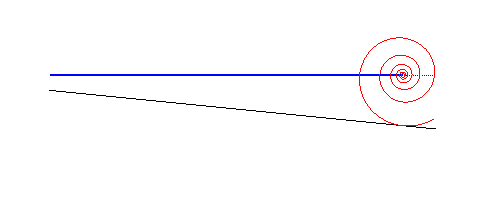
Le cas d'une route rectiligne mais non parallèle à la trajectoire du moyeu donne une roue en spirale logarithmique : .   C'est cette propriété qui est à la base des coinceurs à came pour l'escalade.   Elle permettrait aussi d'imaginer des véhicules à roues formées de portions de spirales logarithmiques roulant sur des routes en dent de scie.
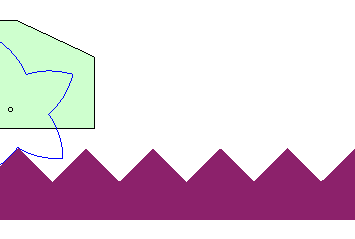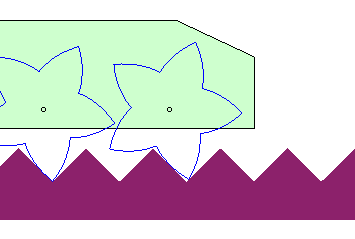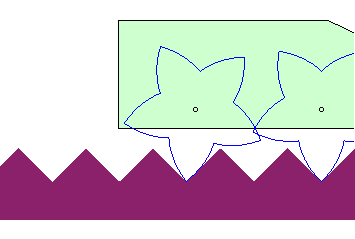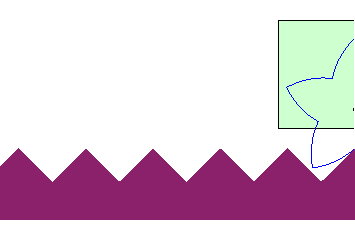Si la roue est une spirale d'Archimède et le moyeu en son centre, la route est une parabole :. Les courbes  et  sont ici des développantes de cercle.
Si la roue est une spirale de Fermat et le moyeu en son centre, la route est une parabole cubique :
Si la roue est une spirale hyperbolique et le moyeu en son centre, la route est une logarithmique : .
Si la roue est une ellipse et le moyeu situé en un foyer, la route est une sinusoïde :  Regarder aussi la roulette de Delaunay.
Si la roue est une ellipse et le moyeu situé au centre, le couple roue-route est : En utilisant la fonction elliptique de Jacobi dn (JacobiDN en maple), l'équation de la route est :  . La courbe  est une courbe de Talbot. Regarder aussi la roulette de Sturm.
Si la roue est une parabole, et le moyeu en son foyer, la route est aussi une parabole ! . La courbe  est une cubique de Tschirnhausen.
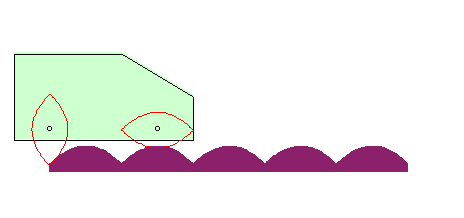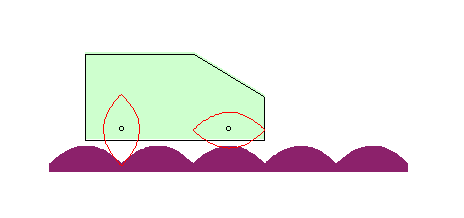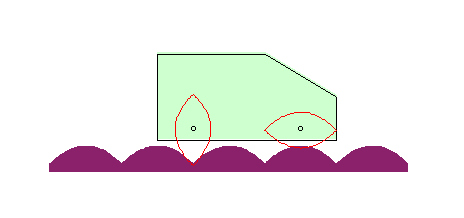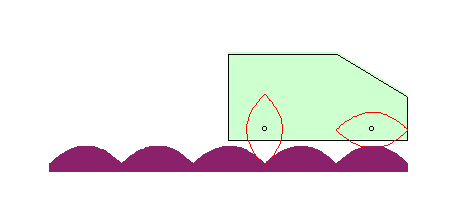Si la roue est une campyle d'Eudoxe, et le moyeu en son centre, la route est encore une parabole :  . La courbe  est une chaînette.
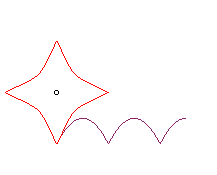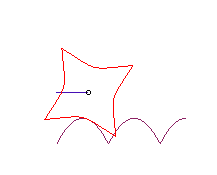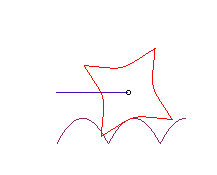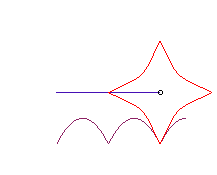Si la roue est une cardioïde et le moyeu situé au point de rebroussement, la route est une cycloïde :. La courbe  est alors un cercle, avec le moyeu sur le cercle.	Notons que les pointes de la cycloïde doivent être légèrement rognées car sinon elles rentrent dans les roues au passage du point de rebroussement.
Si la roue est une spirale tractrice, le moyeu situé au pôle, la route est une tractrice :. La courbe  est alors une spirale hyperbolique, avec moyeu au pôle.
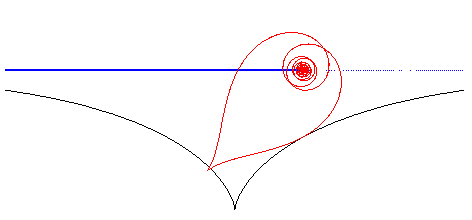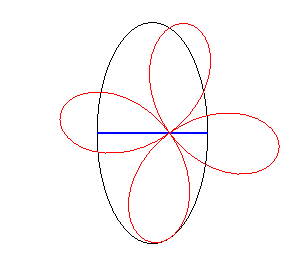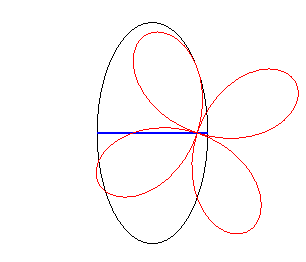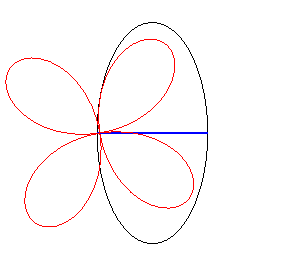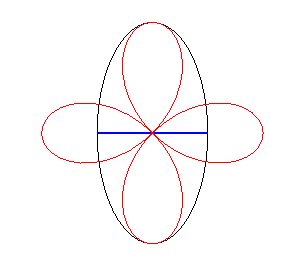
Si la roue est une rosace et le moyeu situé au pôle, la route est elliptique  ; le cas n = 1 n'est autre que celui du haut de ce tableau. Les courbes  et  sont alors des cycloïdes à centres. Dans le cas d'une roue en conchoïde de rosace, la route est une trochoïde ayant subi une affinité. Voir ici le cas de l'oeuf double.	Cas n = 2
Si la route est circulaire, et que le moyeu décrit une tangente au cercle, la roue est une spirale de Norwich inverse. (Rappelons que si le moyeu décrit un diamètre du cercle, la roue est circulaire !)

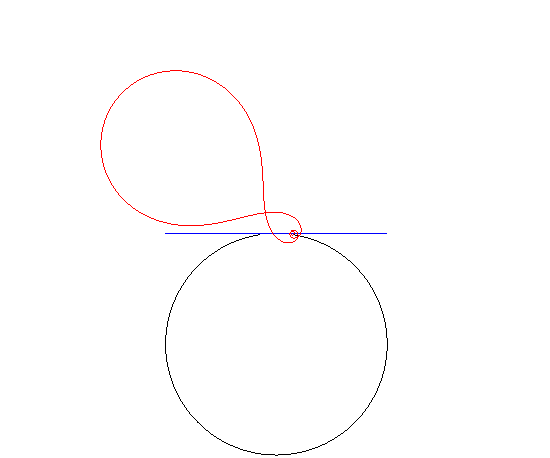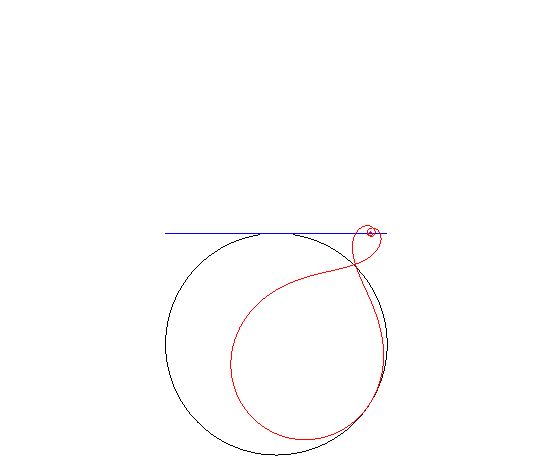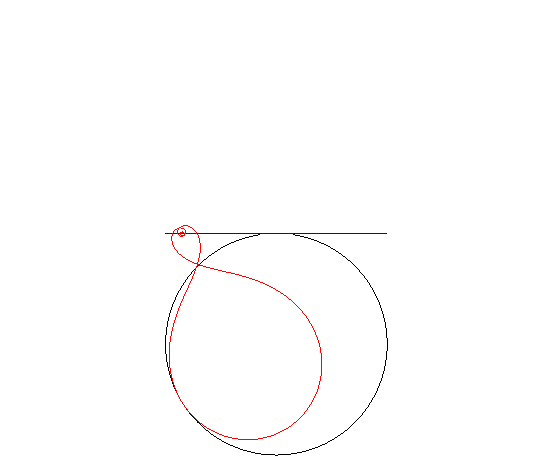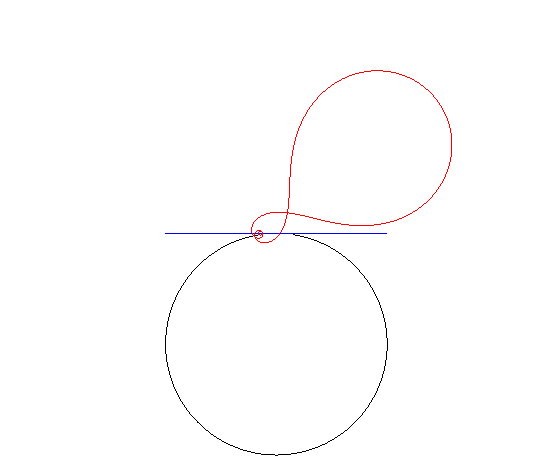Si la roue est une spirale sinusoïdale de paramètre n, la route est une courbe de Ribaucourt de paramètre 1/n, et la courbe  une spirale sinusoïdale de paramètre n/(1 – n).

On retrouve plusieurs exemples donnés ci-dessus :
 

n	roue	route	(G)
-1/2	parabole	parabole	cubique de Tschirnhausen
-1	droite	chaînette	parabole
1/2	cardioïde	cycloïde	cercle
2	lemniscate de Bernoulli	roulette de Sturm équilatère	hyperbole équilatère

Voir aussi les roues associées à une cubique de Tschirnhausen et plus généralement, les roues associées aux courbes de poursuite.

Comparer avec les roulettes à base rectiligne.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL , Alain ESCULIER 2013