Plan projectif

PLAN PROJECTIF (RÉEL)
Projective plane, projektive Ebene

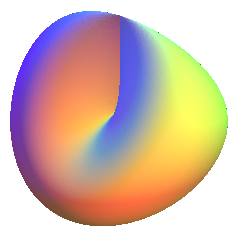
Plan projectif en surface romaine Plan projectif en bonnet croisé Plan projectif en surface de Boy

Surface étudiée par Félix Klein en 1874.

Paramétrisation cartésienne d'une immersion dans

avec

, où les f_isont des polynômes homogènes de degré pair.

Le plan projectif (réel) est l'espace quotient de par la relation de colinéarité.

Mais, plus généralement, on désigne par "plan projectif" tout espace topologique homéomorphe à .

On montre qu'une surface est un plan projectif ssi c'est une surface compacte connexe unilatère (à une face) de genre 1 (peut être découpée une fois sans être séparée en 2).

Le nombre chromatique du plan projectif est 6 (toute carte tracée sur le plan projectif pourra être coloriée avec 6 couleurs au plus, et il existe des cartes nécessitant 6 couleurs).
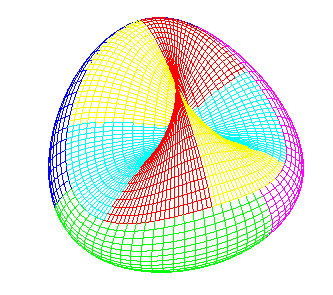
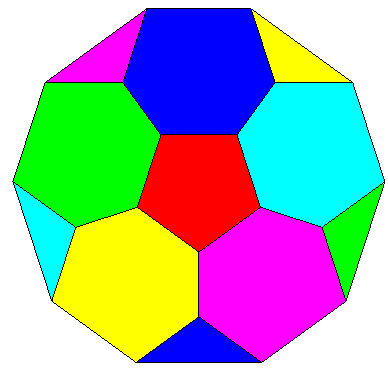
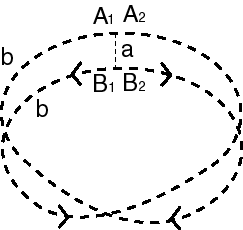
Il existe même des cartes où chaque pays touche les 5 autres, l'une étant représentée ci-contre sur le bonnet croisé, l'autre sur un décagone à côté opposés identifiés avec inversion du sens (cf. ci-dessous).

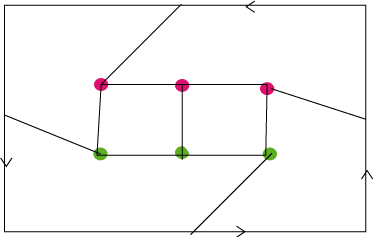
Le problème des trois maisons et des trois usines est soluble dans le plan projectif, contrairement au plan. En d'autre termes, on peut tracer sans croisement d'arêtes le graphe biparti sur le plan projectif.
Idem pour le graphe complet à 5 sommets que le lecteur tracera sans peine.

Voici des modèles classiques du plan projectif :
    - L'ensemble des droites vectorielles de muni de la topologie naturelle
    - Un plan (affine réel) complété par une droite projective (la droite de l'infini)
    - Une sphère où l'on a identifié les points antipodaux
    - Un disque fermé où l'on a identifié les points antipodaux de la circonférence

   - Un disque fermé dont 2 demi-circonférences sont identifiées, avec le sens indiqué (revient à la construction précédente)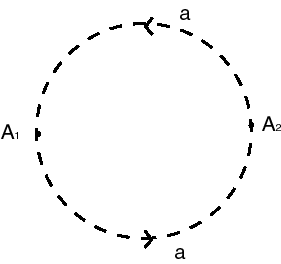

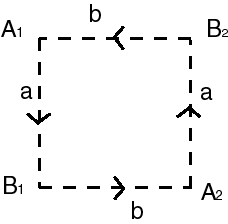
   - Un carré plein dont on identifie les côtés opposés avec inversion du sens.
Ceci revient exactement à la construction précédente, mais permet de voir le lien avec le ruban de Möbius dans la caractérisation suivante (le ruban étant obtenu, lui, en identifiant un seul couple de côtés opposés).

   - Un ruban de Möbius dont les deux demi-bords sont identifiés en sens contraire. (Si on les identifie dans le même sens, on obtient une bouteille de klein).

   - Un ruban de Möbius que l'on ferme avec un couvercle homéomorphe à un disque. Un ruban de Möbius est donc un plan projectif troué.
Pour montrer cela partons de la représentation triangulaire du ruban de Möbius, et courbons-la en croissant. On voit alors apparaître le plan projectif avec son trou circulaire...

- le polyèdre étoilé ayant les mêmes arêtes que l'octaèdre dénommé tétrahémihexaèdre.

On ne peut pas représenter le plan projectif dans sans auto-intersection ; les 4 immersions classiques du plan projectif dans sont :
    - le bonnet croisé (la plus simple)
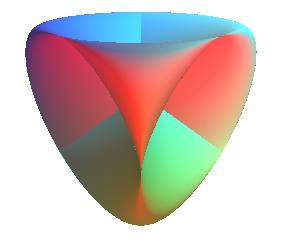
    - la surface romaine (la première découverte historiquement)
    - la surface de Boy (plus complexe, mais sans "point-pince", contrairement aux deux premières)
    - la surface d'Henneberg, qui est de plus une surface minimale.

Les équations données en en-tête sont celles des surfaces de obtenues par immersion du plan projectif.
Pour , on obtient le bonnet croisé,
Pour , la surface romaine,

et pour , on obtient la surface de Boy (équations d'Apéry).
La surface de Véronèse réalise un plongement du plan projectif dans .

Voici 2 constructions du plan projectif imagées à partir du bonnet croisé.

Un ruban de Möbius (avec auto-intersection, mais il y bien un bord, une face)

+ un disque (avec auto-intersection, mais il y bien un bord et deux faces)

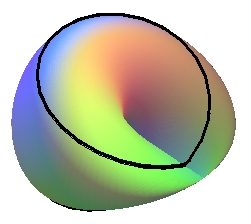
= un plan projectif

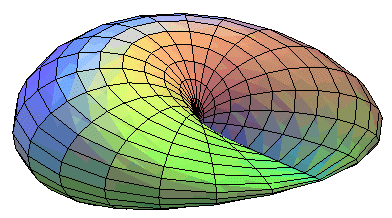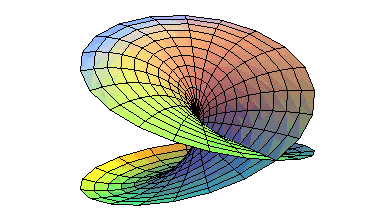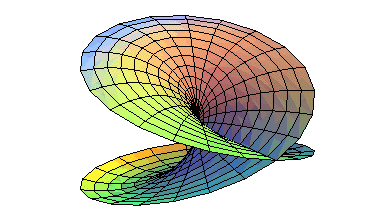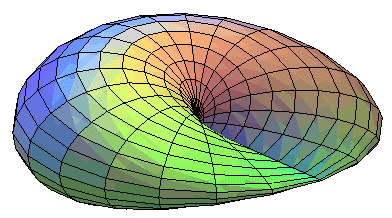
Un disque se déforme de sorte que les points deux demi-circonférences viennent se rencontrer :

ceci...

...équivaut bien à ceci !

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres

- Un disque fermé dont 2 demi-circonférences sont identifiées, avec le sens indiqué (revient à la construction précédente)
- Un carré plein dont on identifie les côtés opposés avec inversion du sens. Ceci revient exactement à la construction précédente, mais permet de voir le lien avec le ruban de Möbius dans la caractérisation suivante (le ruban étant obtenu, lui, en identifiant un seul couple de côtés opposés).
- Un ruban de Möbius dont les deux demi-bords sont identifiés en sens contraire. (Si on les identifie dans le même sens, on obtient une bouteille de klein).
- Un ruban de Möbius que l'on ferme avec un couvercle homéomorphe à un disque. Un ruban de Möbius est donc un plan projectif troué. Pour montrer cela partons de la représentation triangulaire du ruban de Möbius, et courbons-la en croissant. On voit alors apparaître le plan projectif avec son trou circulaire...