RUBAN DE MÖBIUS
Möbius
strip, Möbius-Band
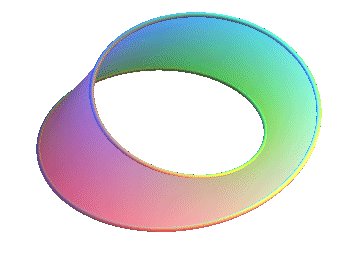


| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
RUBAN DE MÖBIUS
Möbius
strip, Möbius-Band


| Surface étudiée par Listing
et Möbius en 1858.
August Ferdinand Möbius (1790-1868) : astronome et mathématicien allemand. Autres noms : bande, anneau, ceinture de Möbius (ou Moebius). |
| Représentation rotoïdale : voir à
surface
de Möbius.
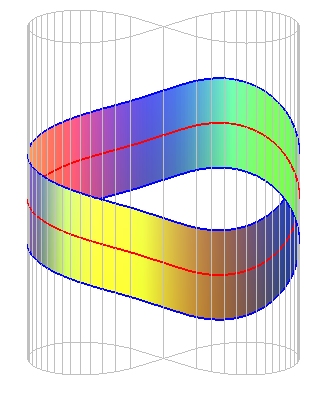
Représentation de Wunderlich : surface enveloppe des plans rectifiants (soit la développable rectifiante) de la courbe rationnelle :
|
Un ruban de Möbius est une surface obtenue
en cousant bord à bord deux extrémités d’un ruban
rectangulaire avec une torsion d'un demi-tour, ou toute surface topologiquement
équivalente.
 |
Programme Maple permettant d'avoir une animation de la
construction ci-contre.
with(plots):a:=1/2:b:=1/3:c:=1/6:d:=2/3:e:=1/3:C:=4/5: x0:=(1+d^2*t^2+2*d*e*t^4+e^2*t^6)/2:x:=(a*t+b*t^3+c*t^5)/x0:y:=(d*t+e*t^3)/x0: z:=-C/x0:t:=tan(tt): a1:=diff(v1,tt):a2:=diff(v2,tt):a3:=diff(v3,tt): v1:=diff(x,tt):v2:=diff(y,tt):v3:=diff(z,tt): b1:=v2*a3-a2*v3:b2:=a1*v3-v1*a3:b3:=v1*a2-a1*v2: n1:=simplify(v2*b3-b2*v3):n2:=simplify(b1*v3-v1*b3):n3:=simplify(v1*b2-b1*v2): dn1:=diff(n1,tt):dn2:=diff(n2,tt):dn3:=diff(n3,tt): c1:=n2*dn3-dn2*n3:c2:=dn1*n3-n1*dn3:c3:=n1*dn2-dn1*n2: facteur:=simplify(sqrt(b1^2+b2^2+b3^2)/(b1*c1+b2*c2+b3*c3)): c1:=simplify(c1*facteur):c2:=simplify(c2*facteur):c3:=simplify(c3*facteur): ds:=simplify(sqrt(v1^2+v2^2+v3^2)): s:=a->evalf(Int(ds,tt=0..a,4))/4: d:=a->plot3d([x/s(a)+u*c1/s(a),y/s(a)+u*c2/s(a),(z+2*C)/s(a)+u*c3/s(a)],tt=-a..a,u=-1/3*s(a)..1/3*s(a),grid=[150,2],style=patchnogrid): n:=40:display([seq(d(k*Pi/2.0001/n,50),k=1..n)],orientation=[-60,80],lightmodel=light2,insequence=true); |
On obtient donc un ruban de Möbius en faisant tourner
régulièrement un segment de longueur constante autour d'un
cercle avec une rotation d'un demi-tour ou plus généralement,
d'un nombre impair de demi-tours ; ces divers rubans sont homéomorphes,
mais non isotopes dans
(on ne peut passer continûment de l'un à l'autre), et pour
chaque nombre de demi-tour, il existe deux classes d'isotopies, images-miroir
l'une de l'autre :
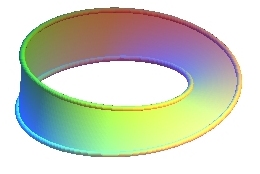
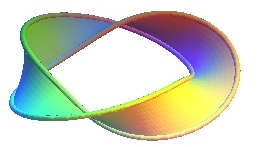
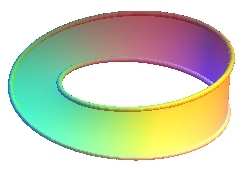
| 1 demi-tour | 3 demi-tours | 9 demi-tours | |
|
|
 |
 |
 |
|
|
 |
 |
 |
De plus, le ruban à trois demi-tours a pour bord
un noeud de trèfle,
et plus généralement,
le ruban à 2p + 1 demi-tours a pour bord un noeud
torique d'ordre (2p + 1, 2).
Ces surfaces rotoïdales,
ne sont pas développables
: on ne pourra donc pas les obtenir à partir d'une feuille de papier
sans déchirures ; inversement, le ruban qu'on obtient naturellement
avec un rectangle de papier n'a pas de paramétrisation simple ;
en voici une due à W. Wunderlich (cf. ci-dessus), dans le cas dextre
à un demi-tour :
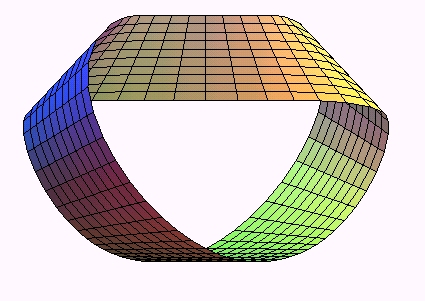 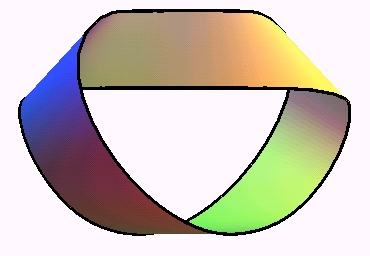 |
| La bande de Möbius-Wunderlich possède la propriété de se développer en un rectangle et de minimiser en tout point l'énergie de déformation. |
Voici un autre exemple de ruban de Möbius développable
de patron rectangulaire, formé de 3 sections cylindriques reliées
par des sections planes :

Ruban à un demi-tour dextre : l'un des cylindres est de rayon double de l'autre et les sections planes sont parallèles. |

Ruban à trois demi-tours dextre. |
Voici deux autres rubans de Möbius développables
obtenus en juxtaposant des bandes découpées sur des cônes.
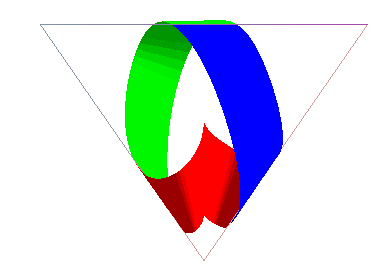 |
Les bandes bleue et verte sont découpées sur des cônes de révolution ; la bande rouge sur deux cônes de révolution ; le patron plan n'est malheureusement pas un rectangle, mais un parallélogramme, d'où le raccord à angle droit. |
 |
Il s'agit ici d'un ruban de Möbius à 3 demi-tours
au lieu de 1, obtenu par trois bandes coniques, les cônes étant
de directrice une courbe de Viviani.
Le bord est autoparallèle, mais le patron plan n'est pas à bords rectilignes. |
 |
Autre exemple avec des cônes de base une lemniscate, montrant le principe de la construction. |
 |
Ce ruban à deux demi-tours (qui n'est donc pas
un ruban de Möbius) est développable puisque tracé sur
un cylindre, de base une lemniscate.
Son patron n'est pas à bords rectilignes, mais les yeux ont tendance
à le penser, d'où notre propension à considérer
cette figure comme impossible !
|
On peut aussi se demander quels rapport longueur / largeur
du patron rectangulaire permettent de construire un ruban de Möbius
sans auto-intersection :
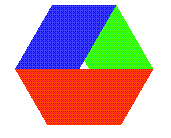
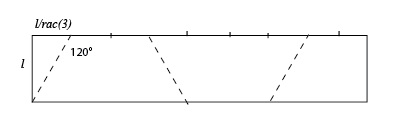
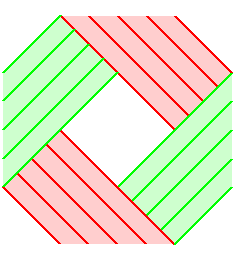
| Voilà déjà un ruban de Möbius
à un demi-tour dont le rapport longueur / largeur est égal
à 3Ö3 (légèrement
supérieur en fait pour plus de clarté).
La vue de dessus en est un hexagone régulier. Le patron est indiqué à droite (les 3 plis en creux). |
 |
 |
|
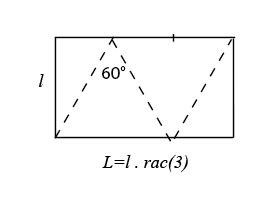
Mais avec un rectangle dont le rapport longueur / largeur est égal à Ö3, vous construirez un ruban de Möbius dont la vue de dessus sera un triangle équilatéral. En 2023 a été démontré qu'on ne peut faire mieux que Ö3. |
 |
 |
 |
 |
 |
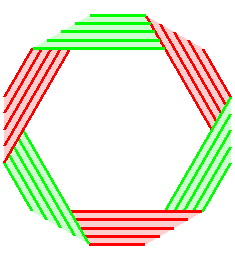 |

Le même que ci-dessus, resserré (presque) au maximum : On ne peut le resserrer plus sans auto-intersection. |

Le même, resserré (presque) au maximum.
|

Le même, resserré au maximum. |
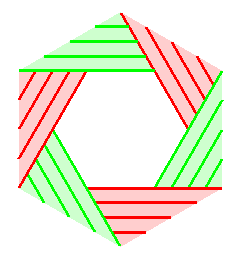
Le même, resserré au maximum.
|
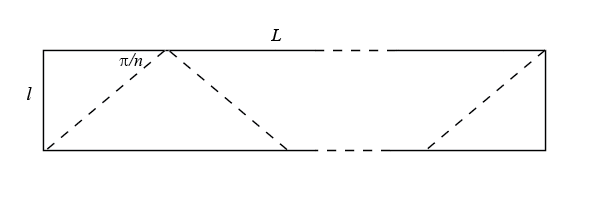
| Donc, excepté le cas n = 3, le ruban de
Möbius à n demi-tours resserré au maximum, de
pourtour un n-gone régulier, nécessite un rectangle |
 |
Lorsque l'on découpe un ruban de Möbius en
son centre, on obtient un seul ruban, mais à deux bords, et à
4 demi-tours (et non 2 demi-tours comme on pourrait le penser) ; si on
le découpe au tiers de la largeur, on obtient un ruban de Möbius
(au centre) et un ruban à 2 bords enlacés :
|
Ruban à deux demi-tours, donc homéomorphe
à un cylindre, fournissant un revêtement à deux feuillets
du ruban de Möbius :
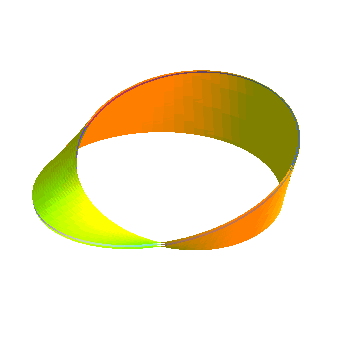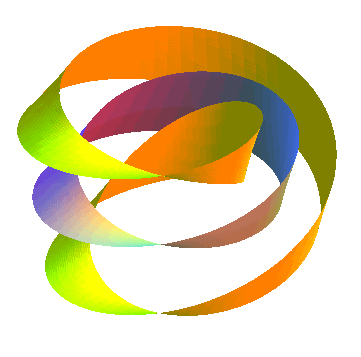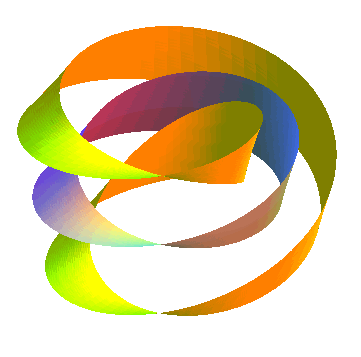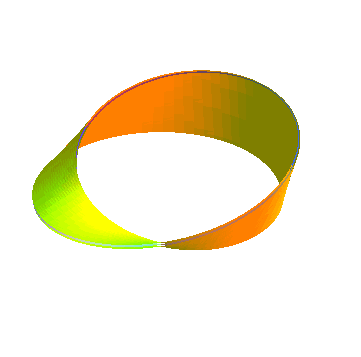 |
De même que la bouteille
de Klein ne peut être représenté dans
sans auto-intersection, le ruban de Möbius ne peut être représenté
dans le plan sans auto-intersection.
| Le ruban de Möbius est une surface qui peut être caractérisée par le fait qu’elle possède une seule face (autrement dit elle est unilatère, donc non orientable), un bord unique et qu'elle est de genre 1 (à savoir qu'une courbe fermée tracée dans son intérieur peut la laisser connexe, mais pas deux). | 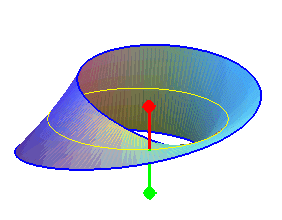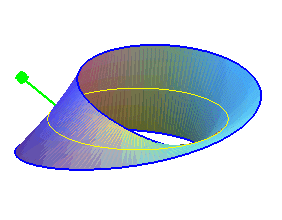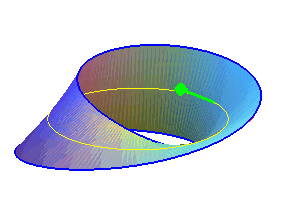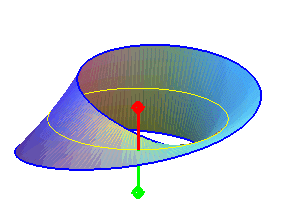 |
| On obtient aussi topologiquement un ruban de Möbius
en identifiant les côtés opposés d’un rectangle avec
inversion du sens.
Le segment orienté [A1 B1] est identifié avec [A2 B2], de sorte qu'il n'y a qu'un seul bord [A1 B2] connecté avec [A2 B1]. Dans le vrai ruban, A1 = A2 =A et B1 = B2 = B. |
 |
| Si l'on découpe le ruban suivant les pointillés indiqués ci-contre... |
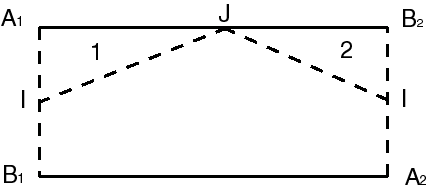 |
| ... et que l'on déplace les morceaux 1 et 2 comme ci-contre... | 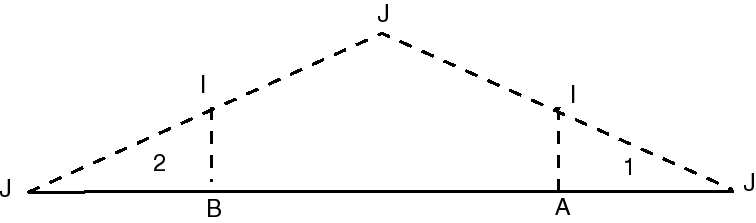 |
| ...on obtient une représentation moins classique
du ruban de Möbius, triangulaire.
Ici, le segment orienté [J1 J2] est identifié avec [J3 J1], de sorte que les 3 points J1, J2, J3 sont identifiés. On voit mieux, ici, le bord unique. |
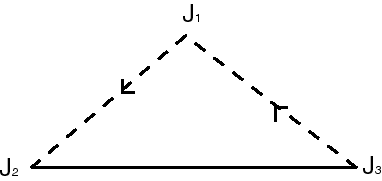 |
| Autre façon d'obtenir un ruban de Möbius : prendre un anneau circulaire et identifier les points symétriques par rapport au centre (un demi-anneau est alors équivalent à un rectangle dont deux largeurs sont identifiées, en sens contraire, ce qui donne bien un ruban de Möbius) |
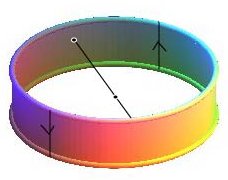 |
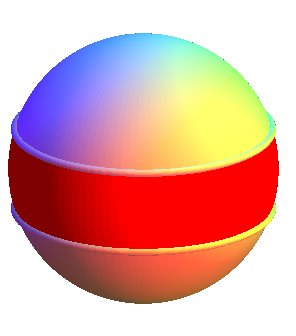
| Considérons alors la sphère où les
points antipodaux sont identifiés, soit un plan
projectif réel. Un bande située entre deux tropiques
est alors un ruban de Möbius. Le complémentaire est un disque
ouvert.
On obtient donc un ruban de Möbius en perçant
d'un trou (ouvert) un plan projectif.
|
 |
| C'est pourquoi un bonnet
croisé percé est un ruban de Möbius (ou plutôt
une immersion d'un ruban de Möbius, à cause de l'auto-intersection)
, voir ci-contre :
Inversement, lorsque l'on coud bord à bord un ruban
de Möbius et un disque, on obtient un plan
projectif réel qui peut s'immerger dans |
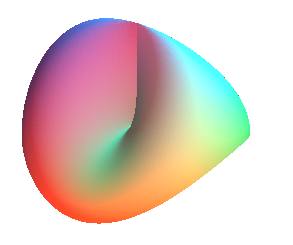 ou ou |
Le nombre chromatique du ruban de Möbius est donc celui du plan projectif, à savoir : 6.
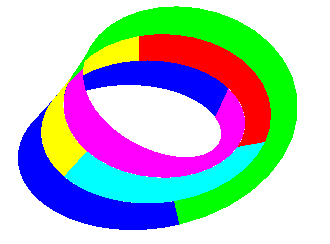
Lorsque l'on coud bord à bord deux rubans de Möbius,
on obtient la somme connexe de deux plans projectifs réels, à
savoir une bouteille de Klein.
 +
+ |
 =
= |
 |
Le ruban de Möbius sans son bord est appelé
le ruban de Möbius ouvert ; il est homéomorphe au plan projectif
moins un point.
| Le ruban de Möbius peut être représenté par une réunion de trois polygones non coplanaires, forcément non convexes, comme ci-contre (voir le polyèdre de Brehm) : |
 |
Voir aussi le bord du ruban de Möbius à 3 demi-torsions, qui est un noeud de trèfle et le faux ruban de Möbius sur le tore.
Le graveur M.C.
Escher a beaucoup travaillé sur le ruban de Möbius :

Le célèbre ruban de Möbius d'Escher. |
 il obtient ainsi un seul ruban, noué en noeud de trèfle, à 6 demi-tours. |
 |
 |
| Les célèbres cavaliers d'Escher sont représentés sur un ruban à deux demi-tours, donc à deux faces (colorées en gris et beige) et deux bords, mais la fusion centrale qui simule l'identification entre deux segments de chacun des deux bords (indiqués en vert) en fait un vrai ruban de Möbius topologique à une seule face, et un seul bord, indiqué en rouge (cf. le slip de Möbius) | Même principe pour ces cygnes à faces noire et blanche. |
| Ruban de Möbius tressé avec un seul brin par Juan Pablo Baudry. | Ruban de Möbius à 3 demi-tours noué
en noeud de trèfle.
Université de Flensburg. |
|
|
|
 |
 |
Comme pour les anneaux
de Borromée, la symbolique du ruban de Möbius est forte,
d'où les nombreux logos :

Logo des produits recyclés : dextre à 1 demi-tour, cf. le ruban à 3 cylindres ci-dessus |
Logo du Léman Express, RER de Genève ruban senestre à 1 demi-tour |

Logo commerzbank ruban senestre à 3 demi-tours |

Logo de l'institut suisse de la propriété intellectuelle, dont l'intitulé est écrit dans les 4 langues nationales. |

Logo d'une université allemande ruban senestre à 3 demi-tours |
|
Société mathématique du Canada
|
Logo E3A : deux rubans dextres à 3 demi-tours, formant un hexagramme |

 |
 |

Le logo de Renault est un ruban à deux demi-tours, donc n'est pas un ruban de Möbius |
 |

Senestre à 3 demi-tours
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL , Jacques MANDONNET , Samuel BOUREAU, Alain ESCULIER, Christoph SOLAND 2019