Hypotrochoid

HYPOTROCHOID

hypocycloïde raccourcie avec q = 7/3 hypocycloïde allongée avec q = 7/3

From the Greek hupo "under" and trokhos "wheel".

Complex parametrization: , i.e. where a is the radius of the base circle, b = a / q that of the rolling circle, and d = k b the distance between the point and the centre of the moving circle (q > 1).
Cartesian parametrization: .
Polar equation: .

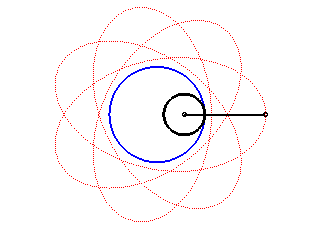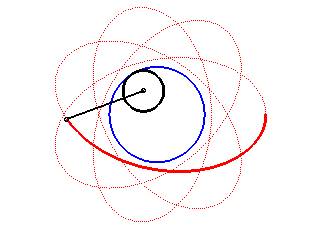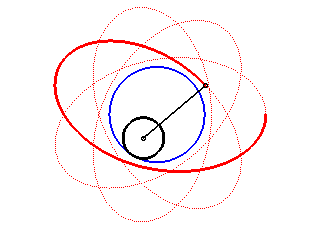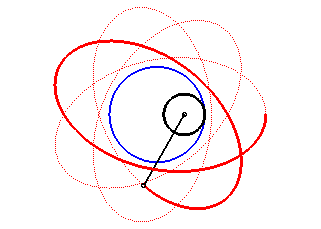
The hypotrochoids are the curves described by a point linked to a circle (C) rolling without slipping internally on a base circle (C₀); therefore, they are the curves obtained with a Spirograph with an internal disk.

Another way of saying the same thing: the hypotrochoids are the roulettes of the movement of a plane over a fixed plane the base of which is a circle and the rolling curve of which is a circle inside the first one.

For d = b, i.e. k = 1, we get the hypocycloids.

If a is replaced by , b by , and d by a – b, the hypotrochoid obtained is identical to the initial one (property called double generation of the hypotrochoid).

We derive from this that if a is fixed but q is changed into and k into , then the hypotrochoid obtained is the homothetic image of the initial one with ratio k. Therefore, we get all the hypotrochoids by considering only the case .

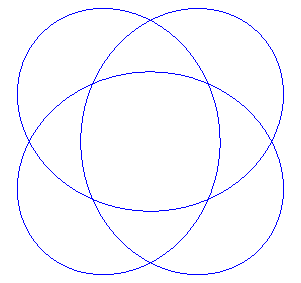
For q = 2, we get the ellipses: .
The corresponding movement of a plane over a fixed plane is also obtained by sliding.

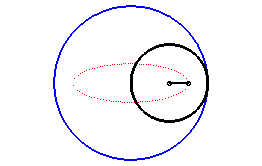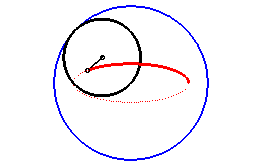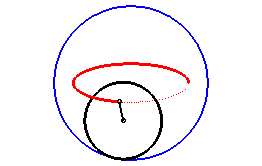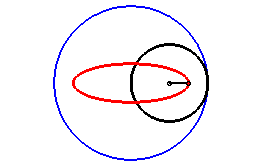For q > 2, the curve is also called curtate hypocycloid if k < 1, and prolate hypocycloid if k > 1.

Be careful, according to the preceding paragraph, in the case 1 < q < 2, the curtate hypocycloids are paradoxically obtained for k > 1 and the prolate ones for k < 1!

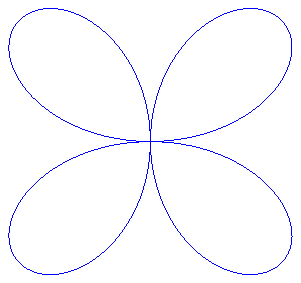
For k = q – 1 (i.e. d = a – b)), we get a rose of index n > 1, and polar equation :

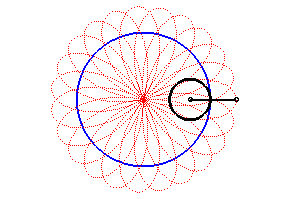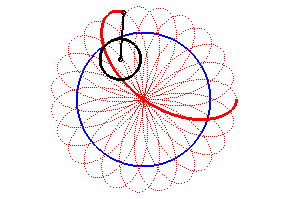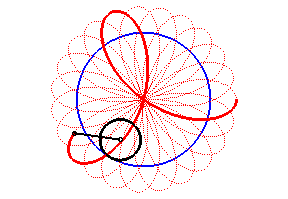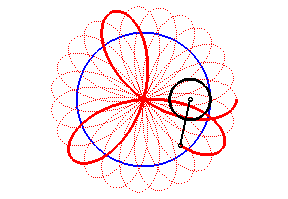Hypotrochoids can also be defined as the trajectories of a movement composed of two circular motions in opposite directions, with complex parametrization () ; they are hypocycloids if , ellipses if , prolate hypocycloids if and or and , curtate hypocycloids if and or and (we can then take , , d = r₂, and therefore ).
The angular speed of the first arm (with respect to the fixed plane) is the quadruple of that of the second arm: we get a hypotrochoid with parameter q = 4 + 1 = 5.

Writing provides the following interpretation of the hypotrochoids: if two bodies are uniform rotation in opposite directions in a fixed plane, then the visible trajectory of one of them in the plane attached to the second one and in translation with respect to the fixed plane is a hypotrochoid.

Shape of the curves in various cases:

Value of q Value of

3 2
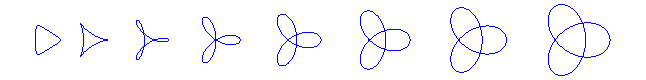
(see the Roman surface)

4 3

5 4

5/2 3/2

7/2 5/2

7/3 4/3

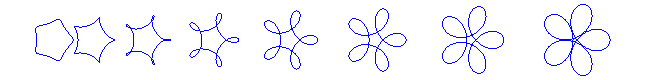The hypocycloid with parameter q = n/m constitutes a "rounded" approximation of the regular polygon of type (n, m); for the portions between two vertices to be as linear as possible, we can consider the limit case where this portion does not have an inflexion point, which corresponds to the case k = 1 / (q - 1); opposite, some views corresponding to this case.
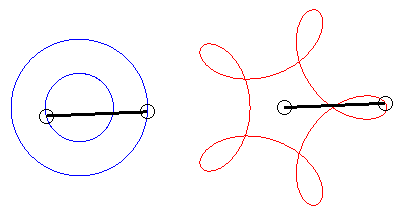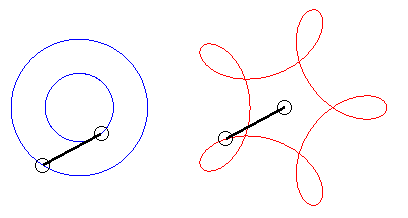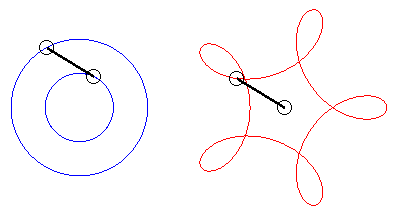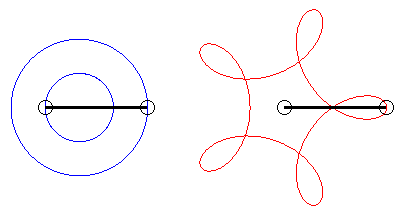
For q = 4, this phenomenon is used in the square watch mechanism.
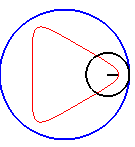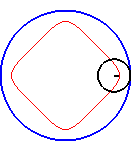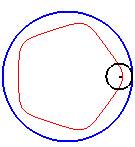
Triangle, square, pentagon and star pentagon hypotrochoids (q =3, 4, 5, 5/2)

Hypotrochoids and epitrochoids form the family of centred trochoids.

The hypotrochoids are also the plane projections of the Caparéda curves, or satellite curves.

See the generalisation to polytrochoids on the page dedicated to the centred trochoids.

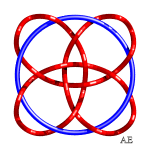
Here are various hypotrochoids in 3D and turned into knots:

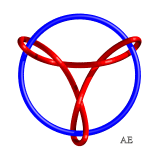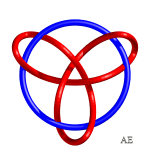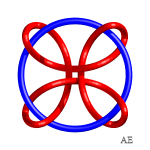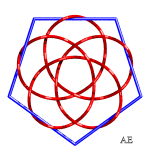Link 9.2.24 Link 9.2.40 See this page

Gear belt shaped like a hypotrochoid by Lévi Capareda during one of his classes of industrial sciences... q = 4, k = 3 q = 4, k = 8

Engraving by J. Mandonnet

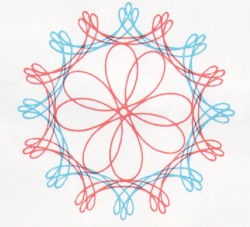
Drawings of Spirographs
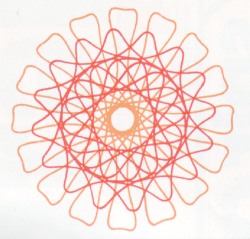A marine Spirograph!

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

Hypotrochoids can also be defined as the trajectories of a movement composed of two circular motions in opposite directions, with complex parametrization () ; they are hypocycloids if , ellipses if , prolate hypocycloids if and or and , curtate hypocycloids if and or and (we can then take , , d = r₂, and therefore ).	The angular speed of the first arm (with respect to the fixed plane) is the quadruple of that of the second arm: we get a hypotrochoid with parameter q = 4 + 1 = 5.
Writing provides the following interpretation of the hypotrochoids: if two bodies are uniform rotation in opposite directions in a fixed plane, then the visible trajectory of one of them in the plane attached to the second one and in translation with respect to the fixed plane is a hypotrochoid.

Value of q	Value of
3	2	(see the Roman surface)
4	3
5	4
5/2	3/2
7/2	5/2
7/3	4/3