Les polygones réguliers croisés ont été étudiés par Thomas Bradwardine. Polygramme : du grec poly "plusieurs" et gramma "lettre, écriture". Voir aussi : en.wikipedia.org/wiki/Star_polygon

 

Tracé par équation polaire d'un polygone régulier de centre (0, 0) et de sommet (a, 0), à n sommets joints de m en m  :  où  (idée de L. Sautereau).

Un polygone (croisé ou non) est dit régulier s'il est équilatéral et équiangle, autrement dit, si tous ses côtés et ses angles sont égaux entre eux.

CNS : le groupe des rotations le laissant invariant est cyclique d'ordre l'ordre n du polygone (et le groupe des isométries est alors le groupe diédral d'ordre 2n).

Le rayon R et le diamètre d'un polygone régulier sont le rayon et le diamètre du cercle auquel appartiennent ses sommets. Son apothème est la distance du centre aux côtés.

Le problème de la constructibilité à la règle et au compas des sommets d'un polygone régulier connaissant les extrémités d'un diamètre a été résolu par Gauss en 1801 : la condition nécessaire et suffisante est que l'ordre du polygone soit le produit d'une puissance de deux et d'un certain nombre de nombres de Fermat (de la forme ) ; entre 3 et 20 sont donc constructibles les polygones réguliers d'ordres .
Le premier polygone régulier non constructible est l'heptagone. L'heptadécagone est, lui, constructible, et une construction effective a été trouvée par Gauss.

Voici les caractéristiques des premiers polygones réguliers non croisés :
 
 

n		angle	côté en fonction du rayon	apothème en fonction du rayon	aire	nom et symbole de Schläfli	image
3	2					triangle équilatéral {3}
4	2					carré {4}
5	4					pentagone régulier {5}
6	2					hexagone régulier {6}
7	6					heptagone régulier {7}
8	4		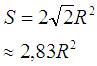			octogone régulier {8}
10	4	144 °				décagone régulier {10}
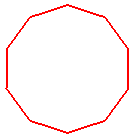12	4	150 °			seul cas, avec celui du carré, où  esr rationnel. Preuve visuelle de ce résultat.	dodécagone régulier {12}

Les n sommets du polygone régulier étant déterminés, on obtient tous les polygones réguliers associés en joignant les sommets de m en m, où m est un entier premier avec n et compris entre 1 et n/2. Le cas m = 1 donne le seul polygone non croisé, qui est convexe.
Il y a donc bijection entre les types de polygones réguliers et les rationnels m/n  strictement supérieurs à 2 ; le symbole {m/n} est appelé le symbole de Schläfli du polygone.
Il existe donc à similitude près  polygones réguliers d'ordre n, où  est l'indicateur d'Euler de n, nombre de naturels premier avec n . Les seuls ordres où il n'existe pas de polygone régulier croisé (ou polygramme) sont 3, 4 et 6, cas où=2.

Si l'on joint les n sommets de m en m, où m est strictement compris entre 1 et n/2 et non forcément premier avec n, on obtient un polygone régulier d'ordre  ; la figure formée de ce polygone et de ses images par la rotation d'angle  itérée, formée de  polygones réguliers est également dénommée polygramme ; il lui est attribuée le symbole de Schläfli {m/n}.

Voici les premiers polygrammes :
 

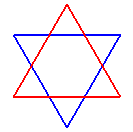
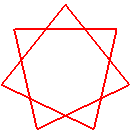
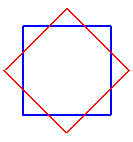
pentagramme {5/2}	hexagramme {6/2},  ou étoile de David	heptagramme {7/2}	heptagramme {7/3}	octogramme {8/2}	octogramme {8/3}
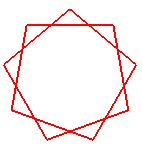
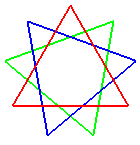
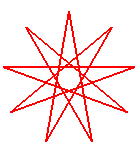
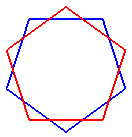
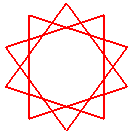
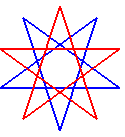
ennéagramme {9/2}	ennéagramme {9/3}, ou étoile de Goliath	ennéagramme {9/4}	décagramme {10/2}	décagramme {10/3}	décagramme {10/4}
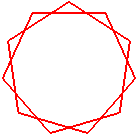
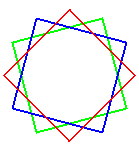
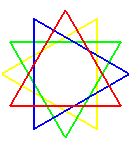
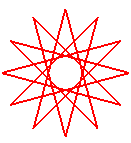
undécagramme {11/2}	undécagramme {11/3}	dodécagramme {12/2}	dodécagramme {12/3}	dodécagramme {12/4}	dodécagramme {12/5}

 

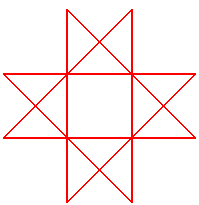
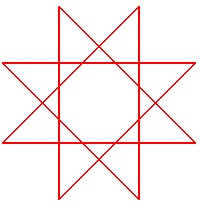
Petit piège : un polygone convexe inscriptible et équiangle est forcément régulier, mais ce n'est plus le cas pour un polygone croisé : l'étoile à huit branches ci-contre est inscrite dans un cercle, a tous ses angles égaux à 45°, mais n'est pas régulière (elle a des côtés de longueur 3 et des côtés de longueur ). Le "bon" polygone régulier est à sa droite.

Voir sur cette page les noeuds et entrelacs associés à ces polygrammes.

Voir aussi les courbes de Goursat, qui ont les mêmes symétries que les polygones réguliers.

Les figures ci-dessous montrent le parallélisme entre les notions de polygramme, d'épycycloïde, de noeud polygrammique, et de solénoïde torique.

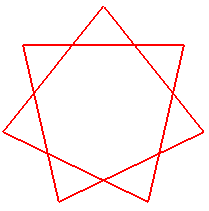
polygramme {n/m}

hypocycloïde de paramètre n/m Voir ausi les hypotrochoïdes

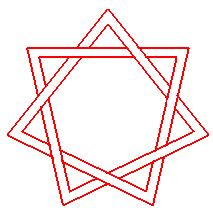
noeud associé au polygramme {n/m}

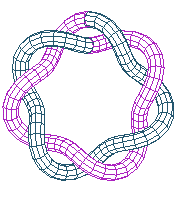
solénoïde torique de paramètre (n,m)

Pièce anglaise heptagonale, dont le contour  n'est pas exactement un heptagone régulier,  mais une courbe de largeur constante

Rosace heptagonale, temple protestant saint-Éloi, Rouen, présentant un heptagramme {7/3}

Palmanova del Frioul

Superbe "crop circle" avec deux ennéagrammes

coupole décagonale de la basilique St Gereon à Cologne

passiflore

Le logo des musées de Florence

Voir d'autres exemple dans ce livre.

Voir aussi les pavages réguliers (par un seul polygone régulier), et semi-réguliers (par plusieurs polygones réguliers), dont voici les 3 plus beaux :
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2023