Rose

ROSE

Curve studied by Guido Grandi in 1723, and by E. W. Hyde in 1875.
Other names: rhodonea, Grandi rose, multifolium.

Polar equation:

(or

) with n positive.
Algebraic curve iff n is rational; if p and q are the numerator and denominator of n, then the degree is p + q if p and q are odd, and 2(p + q) otherwise.
Length of a petal:

.
Area of a petal:

; the area delimited by the whole curve is equal to half that of the circumscribed circle if n is an even integer, and a quarter if n is an odd integer.

The roses are the Brocard transforms of a circle, when the pole is on the circle.

They have a kinematic definition as the loci of a point on a segment line in uniform rotation around its centre, while the point describes the segment with a sinusoidal motion. The polar representation of this motion is: ; we get the equation above with .
This can be obtained in practice by tracing the small oscillations of a pendulum in uniform rotation around a vertical axis.

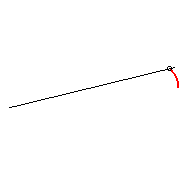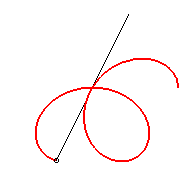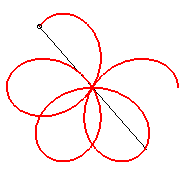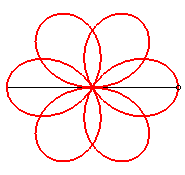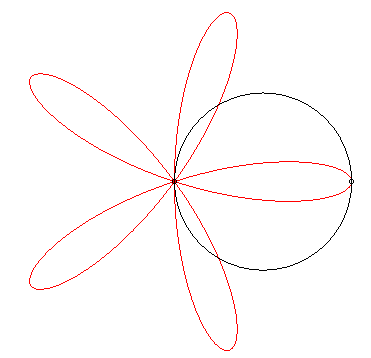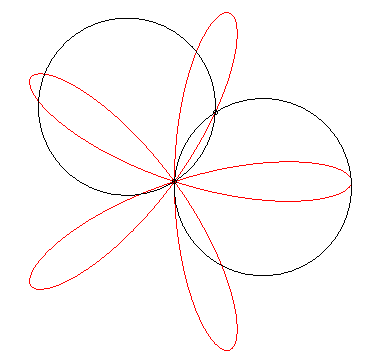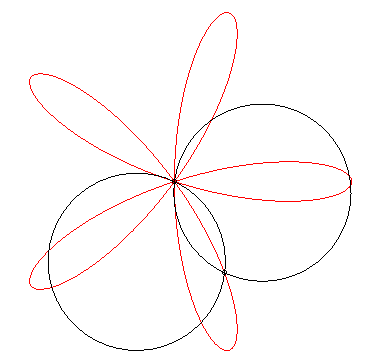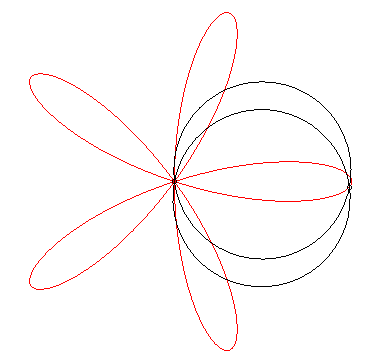
The roses can also be obtained as the trajectories of the second intersection point between a line and a circle in uniform rotation around one of their points, or as the trajectories of the second intersection point of two circles in uniform rotation around one of their points.
In the first case, if the speed of the circle is k times that of the line, then the index of the rose is n = k–1, and in the second case, if the speed of the circle is k times that of the line, then the index of the rose is n = (k – 1) / (k + 1).

The roses are also the centred trochoids passing by their centre; more precisely, such that:
- if the trochoid is defined by a circle rolling on a circle, then the distance between the tracing point and the centre of the moving circle is equal to the distance between the fixed and moving circles.
- if the trochoid is defined as the sum of two circular motions, then the radii are identical.

Even more precisely:
- for n > 1 the rose is a hypotrochoid (base circle with radius , rolling circle with radius , distance between the point and the rolling circle = ), and it is also the pedal of a hypocycloid with respect to O (base circle with radius na, interior circle with radius na/q with ); it can be obtained using a Spirograph.

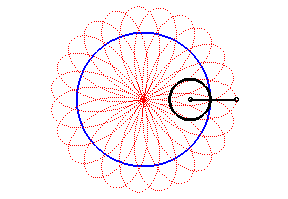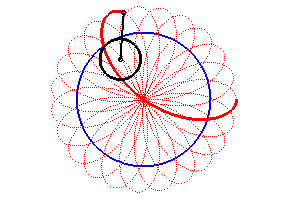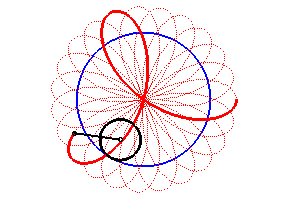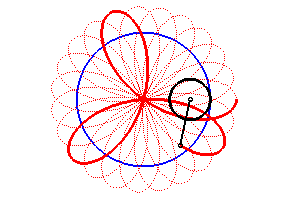
- for 0 < < 1, it is an epitrochoid (base circle with radius , rolling circle with radius , distance between the point and the rolling circle = ), and it is also the pedal of an epicycloid with respect to O (base circle with radius , exterior circle with radius a/pq with ).

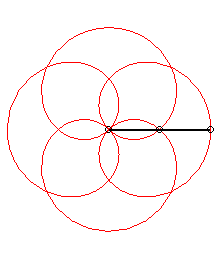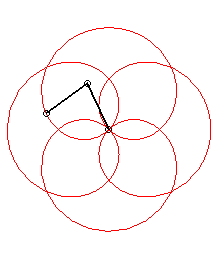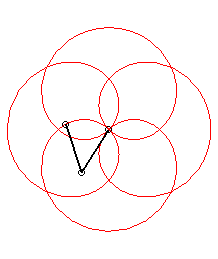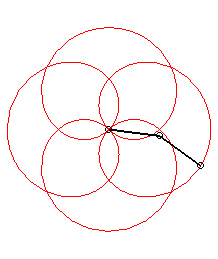
Application: a poi player holds a chain with the same length as their arm, both of them turning at constant speed; when the arm completes p>0 turns, the chain completes q turns (we take q >0 if the movements are in the same direction and q < 0 otherwise).
Then, the end of the chain describes a rose of index .
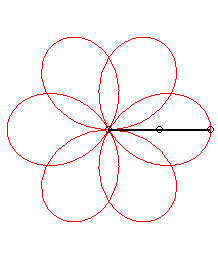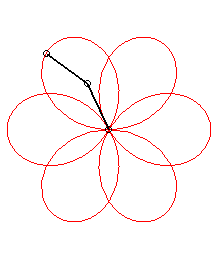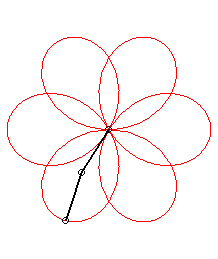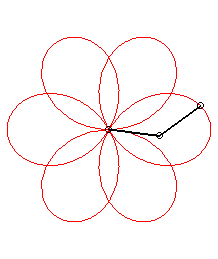
p = 1 q = -5: we get the rose of index 3/2 p = 1 q = -5: we get the rose of index 2/3

If the plane of the circle is winded around a cone with vertex O, half-angle at the vertex a, and axis Oz, then the projection on xOy of this winded circle is the rose: , which provides a construction of the roses starting from a simple circle in the case n < 1.

The roses can also be obtained by projections from the cylindric sine waves, through the 3D basins.

The curve is composed of a base pattern - the petal or branch / leaf / lobe - symmetrical about Ox obtained for :

and transformed by all the rotations by

when k is an integer.
When n is rational with numerator p and denominator q, then the curve is symmetrical about O iff p or q is even.

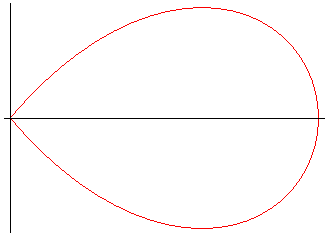
In this case, the curve is composed of 2p petals, copies of the base petal by rotations by and + p.

When p and q are odd, the curve is composed of p petals, copies of the base petal by rotations by .

Examples:

n = 1: circle
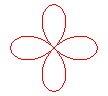
n = 2 :quatrefoil
(or quadrifolium)
n = 3: regular trifolium
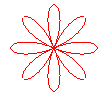
n = 4
n = 5

n = 1/2:
Dürer folium
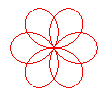
n = 3/2
n = 5/2
n = 7/2
n = 9/2

n = 1/3: trisectrix limaçon
n = 2/3
n = 4/3
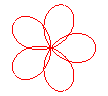
n = 5/3
n = 7/3

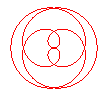
n = 1/4
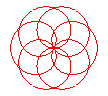
n = 3/4
n = 5/4
n = 7/4
n = 9/4

n = 1/5
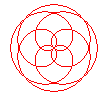
n = 2/5
n = 3/5
n = 4/5
n = 6/5

When n is irrational, the rose is dense in the disk D(O, a).

The roses are views from above of the clelias.

They also are the inverses of the epispirals and the pedals of the centred cycloids.

Compare them to the sinusoidal spirals.

See also conchoid of a rose and radial curve as well as secantoidal .

n = 1: circle	n = 2 :quatrefoil (or quadrifolium)	n = 3: regular trifolium	n = 4	n = 5
n = 1/2: Dürer folium	n = 3/2	n = 5/2	n = 7/2	n = 9/2
n = 1/3: trisectrix limaçon	n = 2/3	n = 4/3	n = 5/3	n = 7/3
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5