Differential equation:
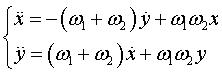 .
.| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CENTRED TROCHOID
| Curve studied by Dürer (1525), Desargues (1640),
Huygens (1679), Leibniz, Newton (1686), de L'Hospital (1690), Jacob Bernoulli
(1690), la Hire(1694), Johann Bernoulli (1695), Daniel Bernoulli (1725),
Euler (1745, 1781).
See alsao: Eric Guiot, Trajectory under harmonic potential and magnetic force. |
| Complex parametrization: Differential equation: 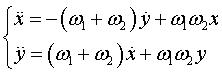 . . |
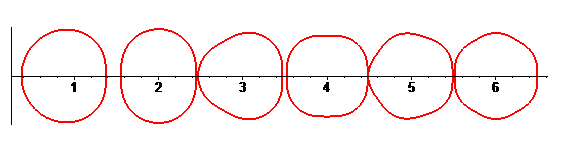 |
 |
|
|
|
| Interprétation électromagnétique
(voir lien
Éric Guiot).
En écrivant l'équation différentielle sous la forme Avec Notons que si Electromagnetic interpretation (see Éric
Guiot link).
|
| The expression |
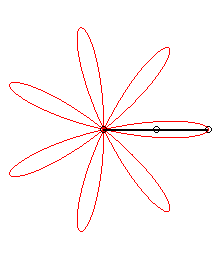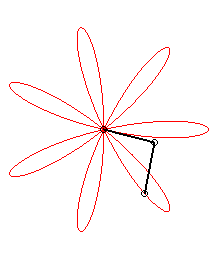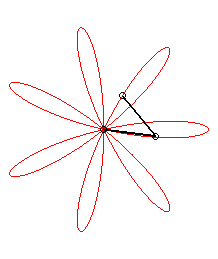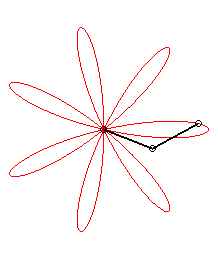 |
| ... or as the middle of two points, when written |
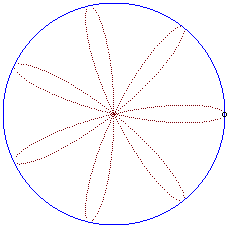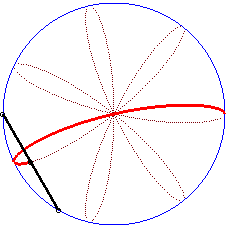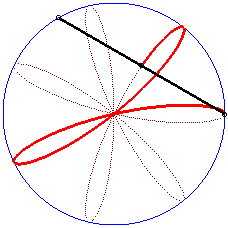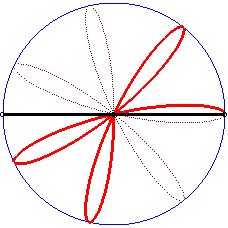 |
Writing  ,
we can separate the circles described by each of the points. ,
we can separate the circles described by each of the points. |
 |
| Writing |
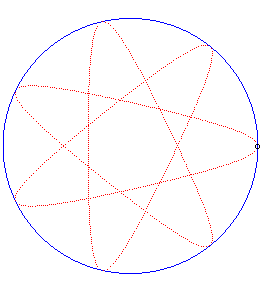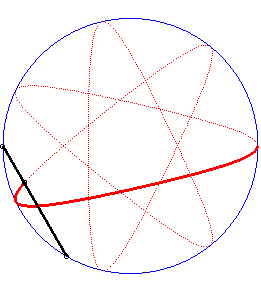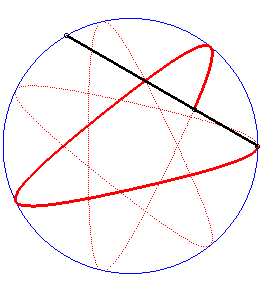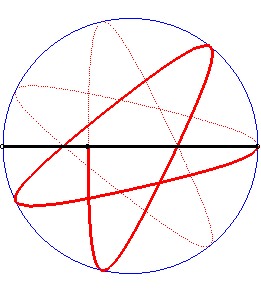 |
| Besides, all the barycentres with fixed coefficients
of two points describing uniform circular motions describe centred trochoids.
Image drawn with geogebra by Andre Chauviere. |
 |
The centred trochoids are also the projections on the plane xOy of the satellite curves.
This notion can be generalised to a finite number n
of uniform circular motions, in any directions, under the name polytrochoid.
|
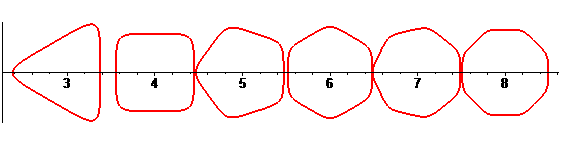
The Ceva trisectrix, Freeth's nephroid and the torpedo are examples of tritrochoids, as well as this elegant dissymmetrical quintifolium: |
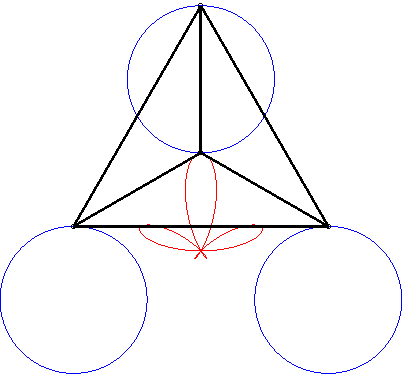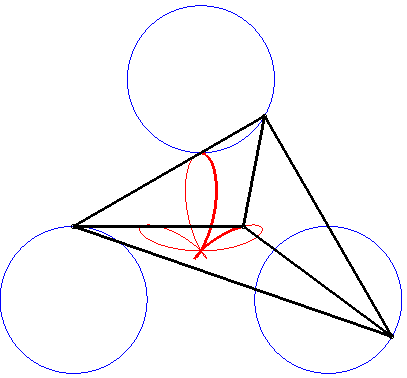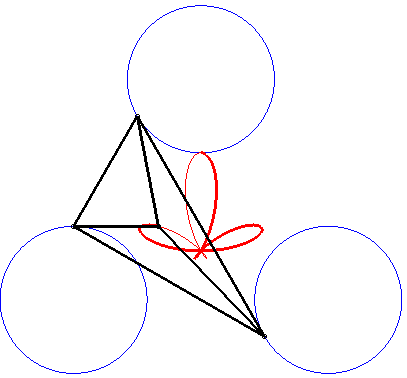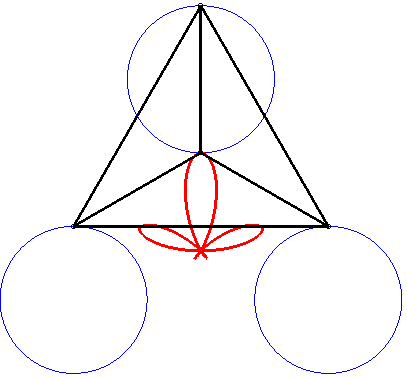 |
An example of a 2n +1-trochoid is the 2n
+1-sectrix of Ceva with complex parametrization .
|
|

The cauldrons describe epitrochoids; if the cauldron turns around itself, the curve described by its occupants is a tritrochoid. |
The 3D generalisation is the notion of spherical trochoid.
See also the any
based trochoids.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2022