Fractal étudié par Gosper en 1973. Bill Gosper (1943 -) : informaticien américain.

Le fractal dénommé "île de Gosper" est le point fixe du L-système dont la fonction de base transforme un hexagone régulier en sept hexagones jointifs, comme indiqué sur la figure :

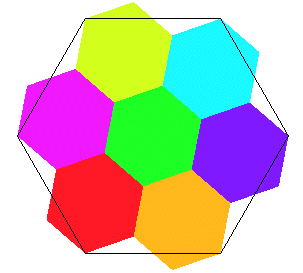
L'île de Gosper est donc l'attracteur de 7 similitudes, de rapport  et d'angle .
Par suite, sa dimension fractale est égale à 2.
Voici les trois premières étapes de construction (étape 4 en en-tête) :

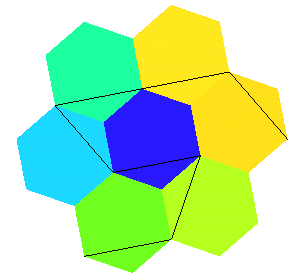
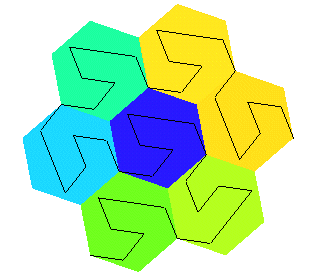
De par sa construction, l'île de Gosper pave le plan, comme la courbe du dragon , en un pavage coloriable en 3 couleurs (cf. le fond de cette page) :

 

Pour son île, Gosper a construit la très élégante courbe remplissante suivante, en générale dénommée courbe de Gosper (mais la courbe limite est exactement égale à l'île ; voir le code Maple à L-Système) :
 

Le contour de l'île de Gosper s'obtient facilement en réunissant les points fixes de 6 L-systèmes à trois barres :

Cette courbe étant l'attracteur de 3 similitudes de rapport , sa dimension fractale est de 2 ln 3 / ln 7 » 1,13.

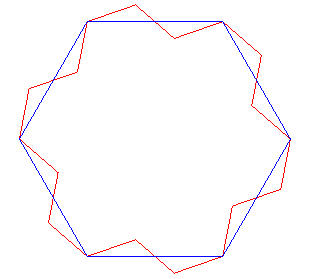
Cette courbe a une généralisation naturelle, comme réunion des points fixes de p L-systèmes à trois barres égales, faisant des angles successifs égaux à l'angle de deux côtés successifs d'un polygone régulier à p côtés (). Le contour de l'île de Gosper généralisée à l'ordre p est donc la réunion de  p attracteurs de 3 similitudes, de rapport  , les deux extrêmes d'angle .
Pour p = 4, cela donne :

avec 3 similitudes de rapport  , les deux extrêmes d'angle . Dimension fractale  2 ln 3 / ln 5 » 1,37.

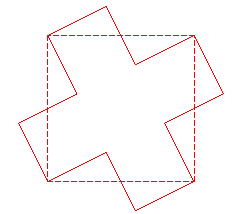
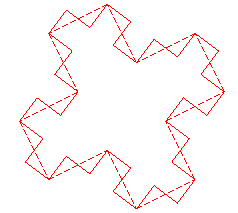
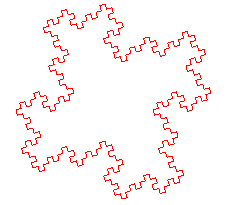
Cette courbe englobe l'île de Gosper d'ordre 4, laquelle se construit globalement comme suit :

Avec 5 similitudes de rapport , la dimension fractale de cette île est bien 2.

Mais le carré et l'hexagone étant les seuls polygones réguliers pavant le plan, les cas 4 et 6 sont les seuls où l'île de Gosper d'ordre p se construit ainsi avec des polygones jointifs.

Voici le cas p = 5 :

L'île ne peut être remplie, à l'aide de similitudes, que lacunairement, ou avec chevauchements :

 

fractal suivant

fractal précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2017