Courbe de koch quadratique

Quadratic Koch curve

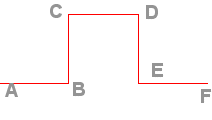
Quadratische Kochkurve

La courbe de Koch quadratique est l'attracteur dans le plan des 5 similitudes directes de rapport 1/3 transformant (A, F) successivement en (A, B), (B, C), (C, D) , (D, E) et (E, F) (voir figure).
Le motif en triangle de la courbe de Koch classique a été remplacé par un motif en carré.
Sa dimension fractale est donc

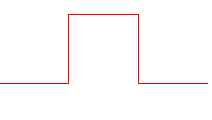
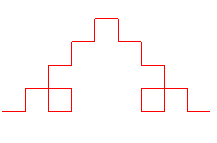
Voici la suite des compacts convergeant vers cette courbe, en partant de [AF] :

4 courbes de Koch quadratiques disposées comme ci-dessous forment une figure appelée croix du sud. Cette croix du sud peut aussi s'obtenir par une méthode de type "fractal de Sierpinski" en partant d'un carré plein et en évidant le complémentaire de 5 carrés homothétiques du carré de départ, formant une croix ; 5 homothéties de rapport 1/3 redonnent bien une dimension fractale de .
Avec cette méthode, ce fractal est connu sous le nom de fractal de Vicsek.

On peut aussi assembler les 4 courbes de Koch quadratiques disposées cette fois comme ci-dessous : Ce fractal peut aussi s'obtenir par une méthode de type "fractal de Sierpinski" en partant d'un carré plein et en évidant le complémentaire de 5 carrés homothétiques du carré de départ ; 5 homothéties de rapport 1/3 redonnent bien aussi une dimension fractale de .

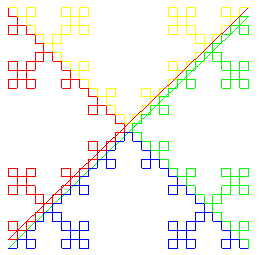Autre bel assemblage (voir aussi le titre ci-dessus) :

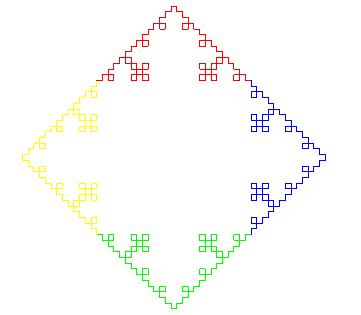Variante : on retourne les deuxième et quatrième étape : les courbes intermédiaires n'ont plus de point double (mais pas la courbe finale !). La dimension fractale est évidemment la même.

fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres

4 courbes de Koch quadratiques disposées comme ci-dessous forment une figure appelée croix du sud.	Cette croix du sud peut aussi s'obtenir par une méthode de type "fractal de Sierpinski" en partant d'un carré plein et en évidant le complémentaire de 5 carrés homothétiques du carré de départ, formant une croix ; 5 homothéties de rapport 1/3 redonnent bien une dimension fractale de . Avec cette méthode, ce fractal est connu sous le nom de fractal de Vicsek.

On peut aussi assembler les 4 courbes de Koch quadratiques disposées cette fois comme ci-dessous :	Ce fractal peut aussi s'obtenir par une méthode de type "fractal de Sierpinski" en partant d'un carré plein et en évidant le complémentaire de 5 carrés homothétiques du carré de départ ; 5 homothéties de rapport 1/3 redonnent bien aussi une dimension fractale de .