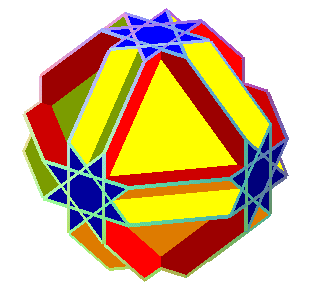
grand cuboctaèdre tronqué	cuboctaèdre cubitronqué
Famille	polyèdre étoilé semi-régulier (ou uniforme U20), ou polyèdre de Badoureau	idem U16
Étymologie	cf. parenté avec le cuboctaèdre tronqué	"cuboctaèdre tronqué" par sa parenté avec celui-ci (voir ci-dessous), et cubitronqué car deux faces du même type se coupent à angle droit ?
Dual
faces	12 carrés, 8 hexagones et 6 octogones étoilés	8 hexagones  6 octogones  6 octogones  étoilés
Sommets	48 sommets , de code de Schläfli  4.6.8/3	48 sommets , de code de Schläfli  6.8.8/3
Arêtes	72 arêtes	idem
Construction	voir ci-dessous	voir ci-dessous
Groupe des isométries	celui de l'octaèdre	idem

 

Pour construire un grand cuboctaèdre tronqué, placer au centre de chaque face d'un cube de côté a un octogone de diamètre b avec ; cette valeur est calculée de sorte que la face en jaune ci-dessous soit carrée. Les sommets du grand cuboctaèdre tronqué forment donc un quasi cuboctaèdre tronqué (pour lequel, lui, ). Les coordonnées des sommets du grand cuboctaèdre tronqué peuvent être prises égales à  et permutés.

Pour construire un cuboctaèdre cubitronqué, placer au centre de chaque face d'un cube de côté a un octogone de diamètre b avec  ; cette valeur est calculée de sorte que la face octogonale en rouge ci-contre soit régulière. Les sommets du grand cuboctaèdre tronqué forment donc un quasi cuboctaèdre tronqué (pour lequel, lui,). Les coordonnées des sommets du cuboctaèdre cubitronqué peuvent être prises égales à  et permutés.

 

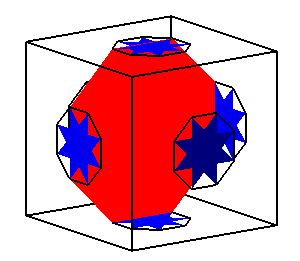Le grand cuboctaèdre tronqué par troncature généralisée des arêtes et des sommets du cube. Partant du cube, on voit ci-contre successivement le cuboctaèdre tronqué, le cuboctaèdre et le grand cuboctaèdre tronqué.

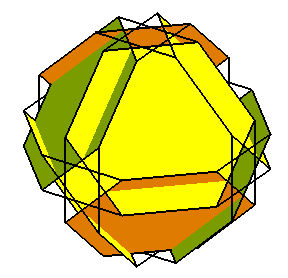
Les 12 faces carrées du grand cuboctaèdre tronqué	Les 8 faces hexagonales du cuboctaèdre cubitronqué
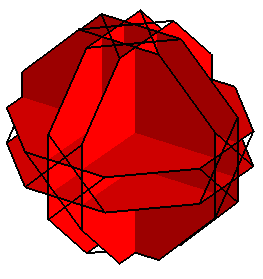
Ses 8 faces hexagonales	Ses 6 faces octogonales

Les sommets du cuboctaèdre faiblement tronqué :

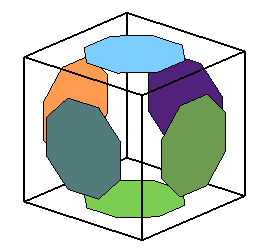
Les sommets du cuboctaèdre tronqué :

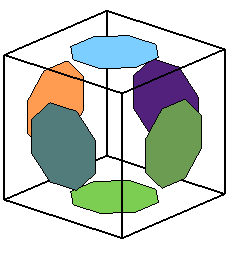
Les sommets du grand cuboctaèdre  tronqué :

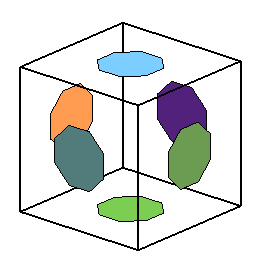
Les sommets du cuboctaèdre cubitronqué :

Le grand cuboctaèdre tronqué a pour caractéristique d'Euler-Poincaré 26 +48 - 72 = 2 et sa surface est orientable (donc équivalente à la sphère !).

Le cuboctaèdre cubitronqué a pour caractéristique d'Euler-Poincaré 20 +48 - 72 = -4 et sa surface est orientable .

Voir ici leurs cousins à symétrie dodécaédrique.

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2009