| |
rhombicuboctaèdre |
gyro-rhombicuboctaèdre |
| Famille |
polyèdre semi-régulier,
ou polyèdre d'Archimède |
IFR (inscriptible à
faces régulières)
polyèdre de
Johnson n° 37, sous le nom de gyro-bicoupole carrée allongée. |
| Historique |
solide connu d'Archimède (IIIe
s. av. J.C.) |
Aurait été connu de Képler.
D'après la légende, aurait été
redécouvert suite à une erreur de construction du rhombicuboctaèdre,
successivement par les mathématiciens anglais, français et
russe : J.C.P. Miller, M. Bert et V.G. Achkinouze dans les années
1930, 1940 et 1950. |
| Dual |
icositétraèdre
trapézoïdal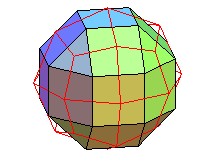 |
gyro-icositétraèdre trapézoïdal
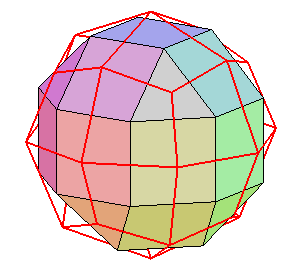
|
| Faces |
18 carrés et 8 triangles |
18 carrés et 8 triangles |
| Sommets |
24 sommets de degré 4, de code
de Schläfli 3.43 |
24 sommets de degré 4, de code
de Schläfli 3.43 |
| Arêtes |
48 arêtes de longueur a ; angle dièdre
entre 2 carrés : 135° ; angle dièdre entre 1 carré
et 1 triangle : 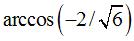 = 144° 44' 08"
= 144° 44' 08" |
48 arêtes de longueur a |
| Patron |
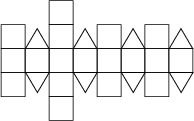
|
|
| Graphe |
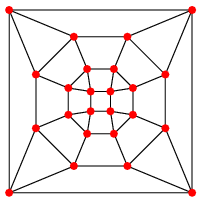
|
|
| Diamètres |
sphère inscrite dans les carrés : 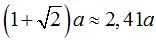
sphère inscrite dans les triangles : 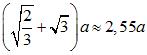
intersphère (tangente aux
arêtes) : 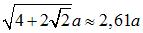
sphère circonscrite :  |
|
| Mensurations |
volume : 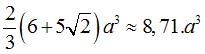 aire :
aire : 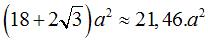
coefficient isopérimétrique : 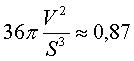 |
volume : 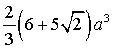 aire :
aire :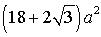 |
| Constructions |
1) cube ou octaèdre tronqué
aux arêtes et aux sommets.
 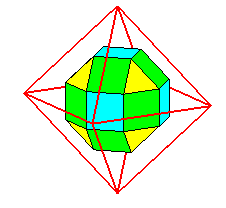
2) cuboctaèdre
fortement tronqué aux sommets
et déformé de sorte que les rectangles deviennent des carrés.
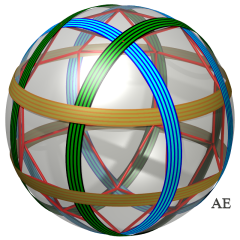
 3) 3 anneaux octogonaux à faces carrées enlacés.
3) 3 anneaux octogonaux à faces carrées enlacés.
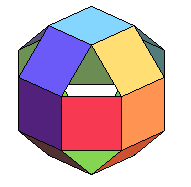
|
Obtenu en faisant pivoter d'un huitième de tour
l'une des coupoles du rhombicuboctaèdre.
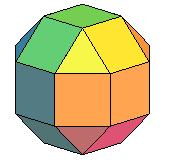 devient devient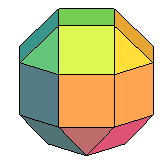
|
| Coordonnées des sommets |
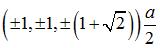 et les permutés.
et les permutés. |
|
| Équation cartésienne de la surface |
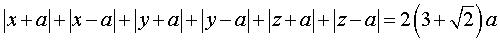
(Bernard
Dupuy) |
|
| Plans de symétrie |
9 |
|
| Axes de rotation |
6 axes passant par les centres de 2 carrés opposés
(1 rotation d'ordre 2 par axe) |
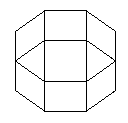
|
| 4 axes passant par les centres de 2 triangles opposés
(2
rotations d'ordre 3 par axe) |
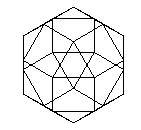 |
3 axes passant par les centres de 2 carrés opposés
(3 rotations d'ordre 4 par axe) |

|
|
|
| Groupe des isométries |
= celui du cube |
|
| Polyèdres apparentés |
L'hexaèdre
tronqué étoilé, qui a les mêmes sommets
Le grand
rhombicuboctaèdre |
|









 devient
devient