Dôme de Bohème

Surface étudiée en 1884 par A. Sucharda, professeur dans une université située à Brno, en... Bohème.
Autres noms : voûte bohémienne, surface de translation circulaire.
Images virtuelles réalisées par Alain Esculier.
Lien : Modèles mathématiques du Laboratoire de mathématiques de Besançon.

Paramétrisation cartésienne : .
Équation cartésienne : .
Équation cylindrique : .
Surface quartique.
.
Aire : .
Nota :
où E (resp. K) est l'intégrale elliptique complète de deuxième (resp. première) espèce.

Animation de la section par des plans z = cte.

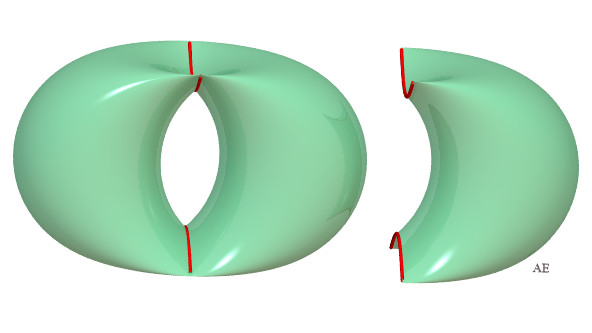
La surface est réunion de deux "cylindres" courbés, de même volume que le cylindre de rayon b et de hauteur 2a. Elle produit deux cavités, de volume inférieur à cause de l'auto-intersection.
A droite, écorché montrant la cavité supérieure.

Étant donné deux plans P et Q perpendiculaires passant par O (ici, yOz et xOz), le dôme de Bohème (S) associé est la surface cerclée engendrée par un cercle (ici de rayon b) dont le centre décrit un cercle fixe de centre O dans P (ici de rayon a) et dont le plan reste parallèle à Q .
Comme pour toute surface de translation, cette définition est symétrique : (S) est aussi la surface engendrée par le cercle de rayon a dont le centre décrit le cercle fixe de centre O de Q de rayon b et dont le plan reste parallèle à P. Cercles de rayon b centrés sur un cercle de rayon a, ou cercles de rayon a centrés sur un cercle de rayon b.

On peut aussi dire que le dôme de Bohème est la somme de Minkovski de deux cercles à plans perpendiculaires.

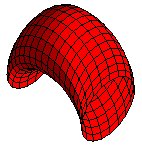
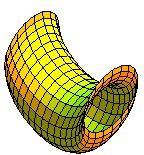
La surface est formée de deux dômes à courbure positive et deux "selles de cheval" à courbure négative (translations de demi-cercles le long de demi-cercles).

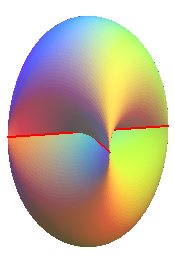
La courbe d'auto-intersection est une portion d'hyperbole, d'équation : . Cette courbe dégénère en deux segments de droite lorsque a = b.

Le cas a = b justement est intéressant pour sa symétrie de rotation d'ordre 4 :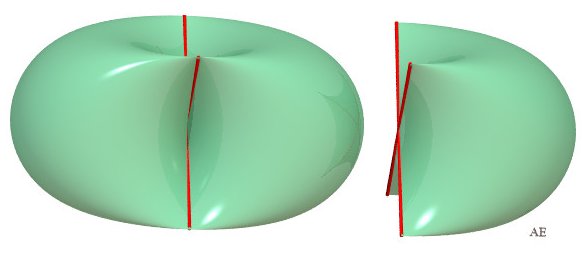

Les lignes de coordonnées de la surface mise sous la forme
forment un double réseau d'ellipses deux à deux orthogonales.

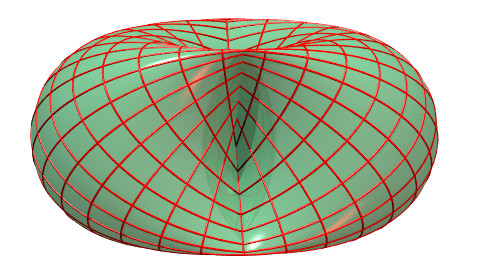Apprenons à faire la différence entre une voûte bohémienne, et une voûte sphérique !

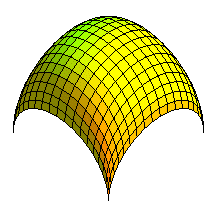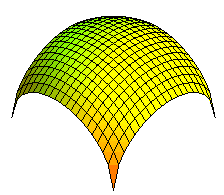Le dôme de Bohème est une projection affine dans du tore de Clifford.
C'est donc une immersion dans du tore topologique, mais ce n'en est pas un plongement.
On peut le voir aussi comme la somme d'un tore et de deux bonnets croisés, comme on le voit sur cette version pseudo polyédrique du dôme de Bohème, ce qui redonne un tore.

Aéroport d'Alicante. Ce site précise que les tubes sont des arcs de cercles identiques, il s'agit donc de voûtes bohémiennes.