Deuxième forme

Troisième forme
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE DE CAYLEY
Cayley
surface, cayleysche Fläche

Deuxième forme |

Troisième forme |
| Surface étudiée par Cayley en 1850.
Arthur Cayley (1821-1895) : mathématicien anglais. Voir la programmation avec Povray sur le site d'Alain Esculier. |
| Forme 1
Équation homogène dite tétraédrique : Surface cubique. Les 4 points coniques sont Les 9 droites sont les 6 et les 3 Dans la version affine associée, d'équation |
 |
La surface de Cayley est la surface définie (à homographie près) par l'équation ci-dessus.
C'est la seule surface cubique dont le groupe des homographies
la laissant invariante est le groupe S4
des permutations de 4 objets (cf. l' invariance par les 24 permutations
des coordonnées )
et c'est aussi la seule surface cubique à posséder 4 points
coniques (maximum possible pour une surface cubique).
Cette surface cubique non lisse
possède 9 droites, qui sont réelles : les arêtes du
tétraèdre formé par les points coniques et 3 autres
droites, qui sont coplanaires.
Une première transformation projective permet de "voir" les 9 droites à distance finie :
| Forme 2
Le changement de coordonnées défini par Équation homogène 2 : Les points coniques sont Les 9 droites sont les 6 arêtes du tétraèdre formé par les points coniques, plus Équation cartésienne affine associée
: |
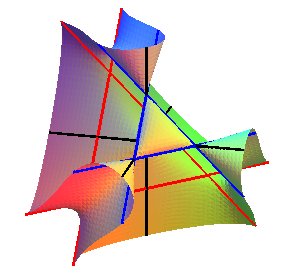 Les axes du repère sont en noir, les trois autres
arêtes du tétraèdre en bleu, et les 3 droites Dans ce cas, on montre que la surface de Cayley est le lieu des points dont les projetés sur les quatre plans-faces du tétraèdre des points coniques sont coplanaires. C'est en quelque sorte la généralisation à l'espace du problème du lieu des points dont les projetés sur les côtés du triangle sont alignés, lieu qui est, lui, le cercle circonscrit au triangle (cf droite de Simson). |
Une deuxième transformation projective permet d'obtenir une vue affine où la surface est invariante par les 24 isométries du tétraèdre régulier (mais 3 des 9 droites sont rejetées à l'infini) :
| Forme 3
Le changement de coordonnées défini par Équation homogène 3 : Les points coniques sont Les neuf droites sont les 6 arêtes du tétraèdre et Équation cartésienne affine associée : Les points coniques sont formant un tétraèdre régulier dont les 6 arêtes sont les droites La rotation d'un huitième de tour définie par Le volume de la partie tétraédrique vaut Sous cette forme, la surface de cayley est une surface tétraédrique de Goursat. |
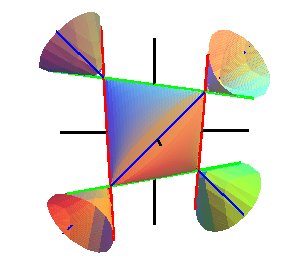 Vue avec les 3 axes de coordonnées (en noir) et les 6 droites incluses. |
La troisième transformation projective ci-dessous
permet d'obtenir la forme dite "pentaédrique" que possède
toute surface cubique (théorème de Sylvester-Clebsch) :
| Forme 4
Le changement de coordonnées défini par Équation homogène 4 : Les points coniques sont Les neuf droites incluses sont les 6 arêtes du tétraèdre et Équation cartésienne affine associée : Les points coniques sont En posant Équation homogène dite "pentaédrique" dans (comparer avec l'équation pentaédrique de la surface de Clebsch). |

Vue avec les 6 arêtes du tétraèdre
(en bleu, jaune et vert) et les 3 droites Lien vers une applet permettant de manipuler la figure formée par les droites incluses dans la surface. |
Ne pas confondre avec les surfaces réglées de Cayley.
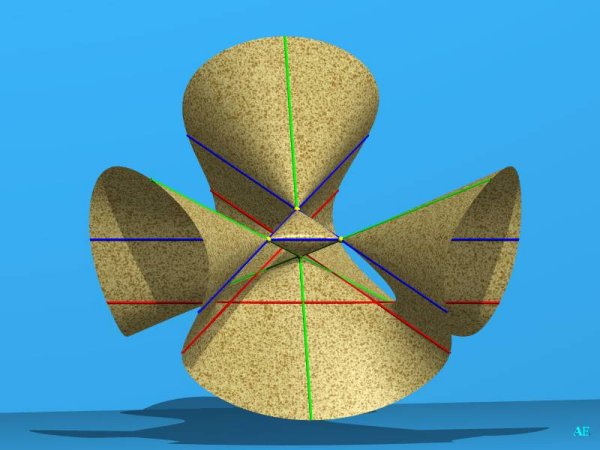
Vue de la forme 2 réalisée par Alain Esculier , la surface ayant subi une affinité de sorte que le tétraèdre central soit régulier
Vue de la forme 4 réalisée par Alain Esculier
Vue de la forme 3
; en rose, les sections par les 3 plans de coordonnées, qui sont
des cercles.
À droite, composé de deux surfaces (anaglyphe à
regarder avec des lunettes rouge/cyan).
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET, Alain ESCULIER 2012