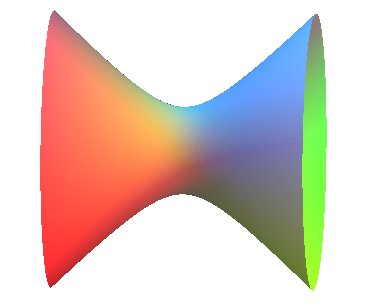
HYPERBOLOÏDE À UNE NAPPE H1
One-sheeted
hyperboloid, einschaliges Hyperboloide
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
HYPERBOLOÏDE À UNE NAPPE H1
One-sheeted
hyperboloid, einschaliges Hyperboloide

| Surface étudiée par Christopher Wren en 1669. |
(voir [Struik, p 195] ) Courbure de Gauss : Cône directeur, qui est aussi le cône asymptote : Volume pour 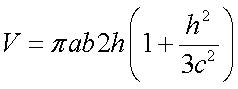 . . |
||||||||||
| Cas de l'hyperboloïde équilatère (a
= b) Première forme quadratique fondamentale : Équation cylindrique : Courbure de Gauss : Courbure moyenne : Aire pour |
L'hyperboloïde à une nappe peut être
défini comme :
1) une quadrique;réglée
ayant un centre de symétrie.
2) la réunion des droites rencontrant trois
droites 2 à 2 non coplanaires et non parallèles à
un plan fixe (lorsqu'elles le sont, on obtient le paraboloïde
hyperbolique)
3) la réunion des droites (MN), les
points M et N se déplaçant à vitesse
constante sur deux cercles parallèles.
Ici, l'hyperboloïde est la réunion des droites
et
et également la réunion des droites
et
.
Les sections de l'hyperboloïde par les plans verticaux
tangents à l'ellipse de gorge sont les couples de droites sécantes
de l'une et l'autre famille de droites incluses.
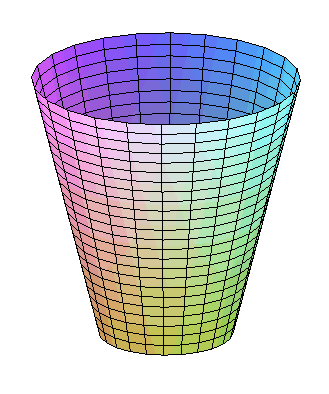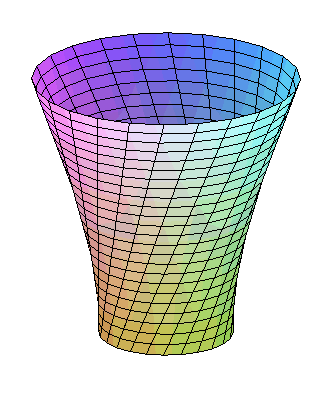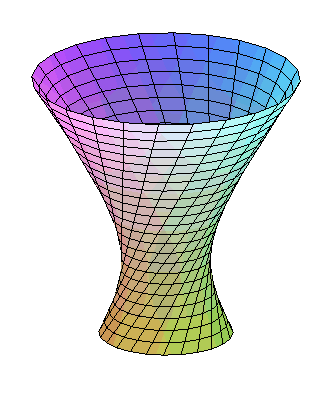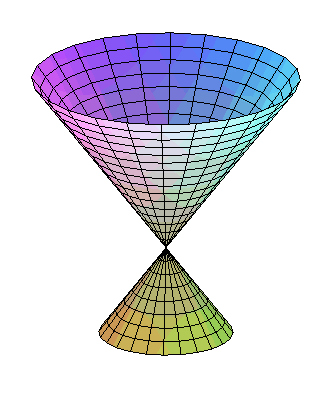
| Paramétrisation de l'hyperboloïde engendré
par les droites joignant un cercle de rayon a à un cercle
de rayon b distant de h du premier et tourné d'un
angle Volume du tronc d'hyperboloïde correspondant : |
 |
L'hyperboloïde à une nappe de révolution
peut être défini comme la surface de révolution engendrée
par une droite non coplanaire avec l'axe de révolution, ou comme
la surface de révolution engendrée par la rotation d'une
hyperbole
autour de son axe non transverse.
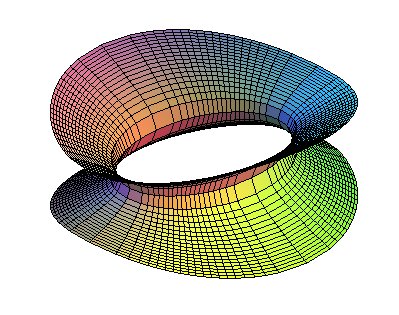 |
Vue des lignes
de courbure de l'hyperboloïde à une nappe ; ce ne sont
des cercles et des hyperboles que dans le cas de l'hyperboloïde de
révolution.
Sinon, ce sont des biquadratiques. |
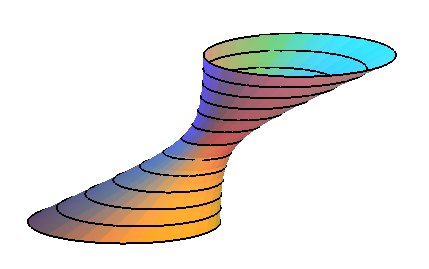 |
Vue de l'une des deux familles de cercles incluse dans tout H1, même non de révolution. |
Voir aussi les hélices de l'hyperboloïde de révolution, ainsi que les courbes de précession constante.
A cause de sa propriété d'être réunion
de droites, l'hyperboloïde à une nappe, comme le paraboloïde
hyperbolique est très utilisé en architecture.

Tours de refroidissement de centrale nucléaire. |
Château d'eau à La Roche de Glun dans la Drôme |

A Kobé au Japon |
 |
|
 |
Voir d'autres belles photos sur la page
du mathouriste.
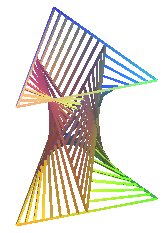    
Structure formée à partir de 2 polygones réguliers à n côtés et 2n génératrices d'un hyperboloïde de révolution (joignant 2 milieux de côté de ces polygones) . Les 3n losanges gauches obtenus sont remplis par des génératrices de paraboloïde hyperbolique. (réalisation : Alain Esculier) |
 |
 |
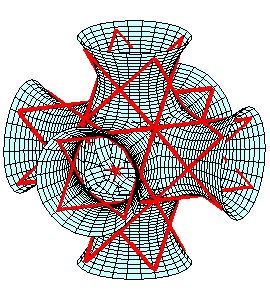 |
| Lorsque deux "espaces solides" ont chacun un mouvement
de rotation uniforme d'axes non sécants, les deux lieux des axes
instantanés de rotation de leur mouvement relatif dans chacun des
espaces (ou "axoïdes") sont deux hyperboloïdes de révolution
qui roulent sans glisser l'un sur l'autre (notion équivalente dans
l'espace à celle de profils
conjugués dans le plan).
Ce beau théorème de cinématique est à l'origine des "engrenages hyperboloïdes" dont un exemple est reproduit ci-contre : Voir ce livre, page 144. |
 |
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2012