WITCH OF AGNESI

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
WITCH OF AGNESI

| Curve studied by Pierre de Fermat in 1630, then by
Guido
Grandi in 1703 and Maria Gaetana Agnesi in 1748.
Other names: cubic of Agnesi, Agnesi curl, versiera (= she-devil in Italian), bell curve of Cauchy. Explanation of these devilments: According to Loria, versiera comes from the Latin versoria (meaning "rope which turns the sail", from the verb vertere, "to turn") ; this name was given by Grandi in reference to the Latin expression: sinus versus. To understand how the primitive sense of turn turned into witchcraft, one should perhaps look at the word opponent, the Italian equivalent of which is avversario. The fact remains that we call this curve witch of Agnesi. Maria Gaetana Agnesi : Italian female mathematician (1718-1799) :  . . |
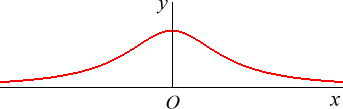 |
| Cartesian equation: Rational cubic with isolated point (located at infinity in the direction of Oy). Cartesian parametrization: Area of the domain bounded by the curve and its asymptote: Volume of the solid of revolution generated by rotating the curve around its asymptote: |
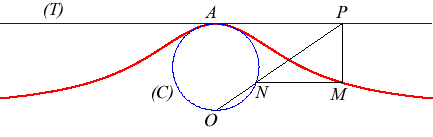
| The cubic of Agnesi is the hyperbolism of the circle
relative to one of its points and the diametrically opposite tangent from
this point.
Here the circle is the circle of diameter [OA], with A(0, a). It is therefore a special case of egg of Granville. |
 |
| Like the anguinea, it is a projection of the horopter. |  |
| The Cartesian equation shows that the witch of Agnesi
is a special case of cubic
hyperbola.
The homographic transformation: In the figure on the right, we used |
The perspective of a witch of Agnesi is a divergent parabola. The witch of Agnesi (in red at the top) is equivalent
|
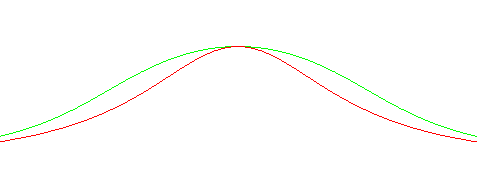
| One shouldn't confuse the witch of Agnesi with the (Gaussian)
bell curve, common in probability, which is transcendental!
But the witch of Agnesi is also used in probability, because it is the curve of the density function of a Cauchy law (hence the name "bell curve of Cauchy"). |
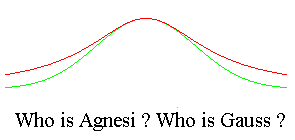 |
| On the other hand, another cubic (in green in the image
on the right) also looks like the witch of Agnesi:
Cartesian equation : Polar equation: This curve is also a special case of cubical hyperbola, but it is not rational. |
 |
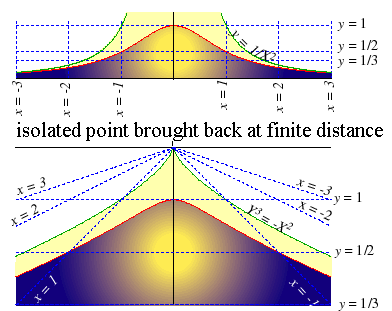
| Particularity of the homogeneous domain limited by the
curve But if we accept that this integral is null (odd function), this center has coordinates Likewise, the part of this domain located to the right of the Oy axis does not have a finite distance center of gravity because |
 |
The witch of Agnesi is also a directrix of Plücker's conoid and Cartan's umbrella.
Compare this curve with the visiera and Külp's quartic.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2019