CATENARY OR FUNICULAR CURVE

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CATENARY OR FUNICULAR CURVE

| Curve studied by Leibniz, Jean Bernoulli and Huygens
in 1691.
In its Latin form catenaria, the name is due to Huygens. Other names: funicular/sail curve. One can also find the name catenoid for affine catenary curves. This must not be confused with the catenoid surface. See also: www.mathouriste.eu/Catenaire/Catenaire_Chainette.html |

The relation between the length 2l, the sagitta
h
and the width 2d
|
Differential equation : Cartesian equation: The axis Ox is its base, the axis Oy is its symmetry axis. Cartesian parametrization: or Curvilinear algebra: Radius of curvature: Intrinsic equation 1: Intrinsic equation 2: Transcendental curve. |
The catenary is the shape taken by an inextensible, homogeneous,
infinitely thin, flexible, massive wire hanging from two points, placed
in a uniform gravitational field. Galileo posed the problem and observed
that the curve followed by the wire was approximately an arc of
parabola, the
approximation improves when you extend the wire. These are Leibniz, Jean
Bernoulli and Huygens who found, independently in 1691, the right equations.
| With the notations of the opposite figure ( This simplifies to |
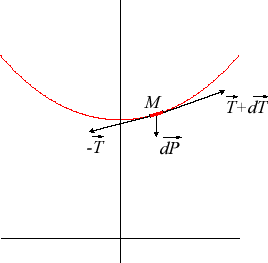 |
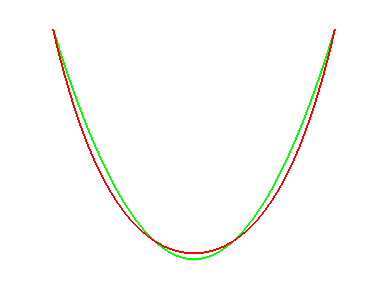
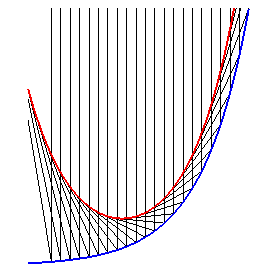
Let us learn how to distinguish catenaries from parabolas:
for an equal length, parabolas are "sharper". |
 |
See the curve
of the suspension bridge, as well as the elastic
catenary, that link the parabola and the catenary.
Like the suspended wire, a vault composed of edge-to-edge
stones holding in place by their own weight also takes the shape of an
upside-down catenary (property called "of the Poinsot vault"-
proof
Brocard part. comp.
p 189):
 |
 |

The "Gateway Arch" in St Louis, Missouri has the shape of a catenary |

Casa Mila rooftop, by the architect Gaudi in Barcelona. |

Parking lot in Lyon |

Dirigible hangar in Ecausseville |
For surfaces of revolution having the same property, see
dome of Bouguer.
On the contrary, the arches of bridges have a parabolic
profile (upside-down suspension bridge...)

The Garabit viaduct has a parabolic arch (and not a circular one, as
it is written on postcards)
The catenary also is the profile of a rectangular sail attached to two horizontal bars, swollen by a wind blowing perpendicularly to these bars, when the proper weight of the sail is neglected in comparison to the force of the wind, hence the name "sail curve" given by Jacques Bernoulli.
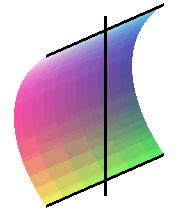
The arc of a curve joining two given points A and B and for which the rotation around a line (D) coplanar with (AB) generates the surface of minimal area is the arc of a catenary of base (D) passing through A and B (see catenoid).
The catenary is still related to the parabola in the sense that it also is a parabolic roulette of Delaunay: the locus of the focus of a parabola rolling without slipping on a straight line.
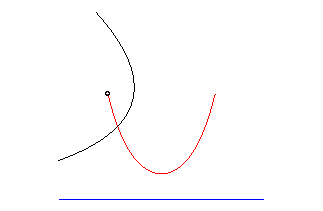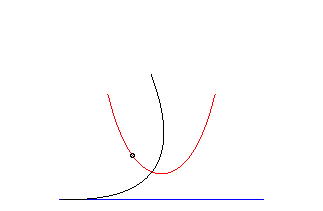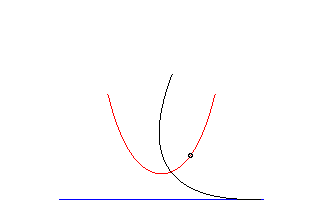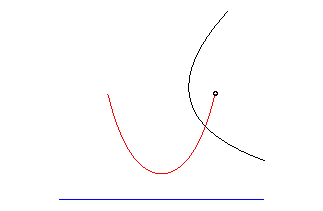
The catenary is the only curve the radius of curvature of which equals the normal; the catenary is therefore the meridian line of the only surface of revolution with zero mean curvature: the catenoid; we deduce from this that the catenary is also a special case of Ribaucour curve.
The catenary is also the caustic by reflection of the exponential curve y = a ex/a for rays parallel to Oy.
| The evolute
of the catenary is the curve with parametrization: |
 |
| The principal involute of the catenary is the tractrix
the asymptote of which is the base of the catenary.
We derive from this that a point, fixed in the plane linked to a line rolling without slipping on the catenary, coinciding with the centre O of the latter when the line is tangent to its summit, describes the line Ox. |
 |
Thanks to this phenomenon, polygonal wheels can roll on arcs of catenaries while their centres move on a straight line.
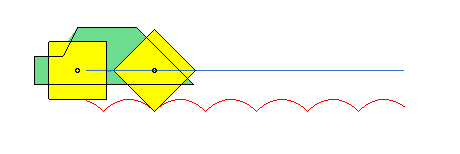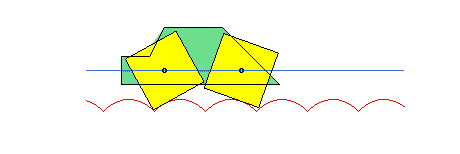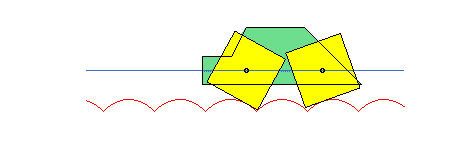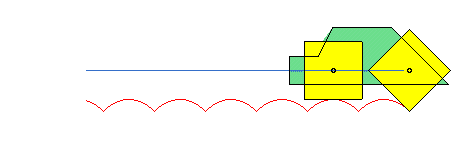
See also the alysoid, the elastic catenary, the curve of the suspension bridge, the catenary of equal strength, the electro-dynamic catenary, the skipping rope curve, and the lintearia.
The notion of catenary can be generalised to a wire
placed on a surface, with the special case of the spherical
catenary.

 |

The wires of the funicular form a catenary when they are free, but the top of the funicular describes an elliptic arc.... |
 |
 |

Are these catenaries?
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017