
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
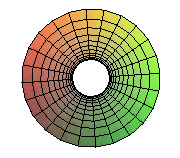
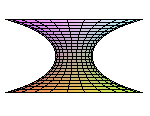
CATÉNOÏDE
Catenoid,
Katenoid
 |
 |
 |
| Surface étudiée par Euler en 1740.
Le nom vient de catena : chaîne, qui est aussi le nom latin de la chaînette. Autre nom : alysséide, du grec alusion "petite chaîne" (donné par Bour en 1862). |
| Équation cylindrique : Paramétrisation cartésienne : Paramétrisation où les lignes de coordonnées sont les loxodromies faisant un angle Première forme quadratique fondamentale : où Elément d’aire : Deuxième forme quadratique fondamentale : Courbure de Gauss : Aire de la portion pour Volume : |
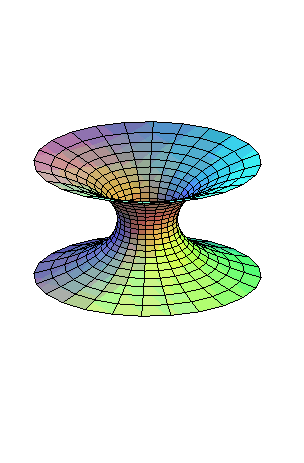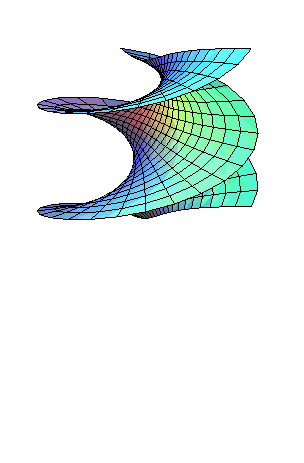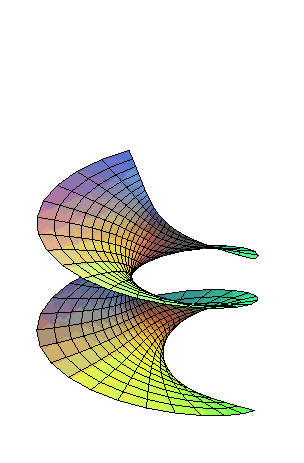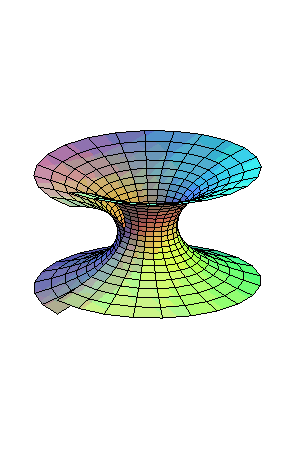
Le caténoïde est la surface de révolution engendrée par la rotation d'une chaînette autour de sa base.
On obtient la paramétrisation
en prenant
et
dans
la paramétrisation de Weierstrass
d'une surface minimale.
| Considérons deux anneaux circulaires parallèles
de diamètres D distants de d ;
On montre que si d/D < 0,66, il existe 3 surfaces minimales s'appuyant sur ces deux anneaux : 2 caténoïdes et la surface dite de Goldschmidt formée des deux disques limités par ces anneaux. On montre que pour d/D < 0,53 la surface d'aire minimale parmi ces 3 est l'une des 2 caténoïdes (en rouge ci-contre) ; mais à partir de 0,53, c'est bizarrement la surface de Goldschmidt qui est d'aire minimale. Et à partir de 0,66, c'est de toute façon la seule : il n'y a plus de caténoïde s'appuyant sur les anneaux. Rem :
|
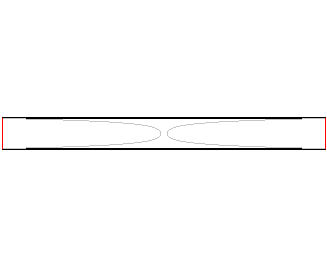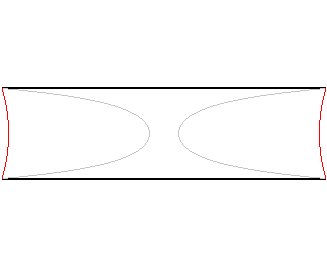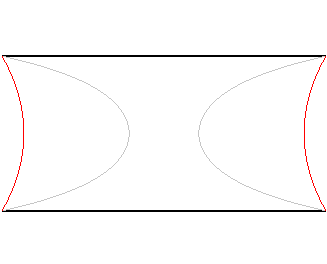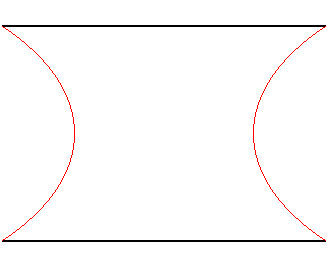 pour cette dernière valeur la méridienne est tangente aux diagonales du rectangle. |
Sur cette photo, la limite théorique d'éclatement de 0,53
semble avoir été nettement dépassée...
|
| Un caténoïde peut être transformé
continûment et isométriquement en un hélicoïde
droit, la surface restant constamment minimale.
Équations de cette transformation : Les surfaces intermédiaires sont les hélicoïdes minimaux. |
 |
Voir aussi le caténoïde
gauche, le trinoïde,
et la révolution axiale de
la chaînette.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019