Roulette de Delaunay

ROULETTE DE DELAUNAY
Delaunay's roulette, Delaunaysche Roulette

Courbe étudiée par Delaunay, 1841 ; Lindelöf, 1861.
Charles-Eugène Delaunay (1816 ; 1872) : astronome français.
Autres noms : chaînette elliptique, parabolique, hyperbolique.

Équation différentielle :

avec e = 1 pour la roulette elliptique (ellipse de demi-axes a et b (a > b)),
e = -1 pour la roulette hyperbolique (hyperbole de demi-axes a et b),

.
Abscisse curviligne :

, d'où la normale :

.
Rayon de courbure :

(de sorte que

, courbure moyenne de la surface de Delaunay associée).
Paramétrisation cartésienne dans le cas elliptique :

où

, e = c / a et E fonction elliptique de deuxième espèce.
Abscisse curviligne :

Longueur sur une période : .
Aire entre la courbe et Ox, sur une période : .
Paramétrisation cartésienne dans le cas hyperbolique :

où , e = c / a et F fonction elliptique de première espèce.
Abscisse curviligne : .
Longueur sur une période : .

On appelle roulette de Delaunay le lieu d'un des foyers d'une conique roulant sans glisser sur une droite ; on la désigne par roulette elliptique, parabolique ou hyperbolique suivant que la conique est une ellipse, une parabole ou une hyperbole.

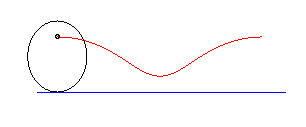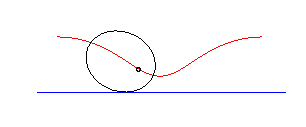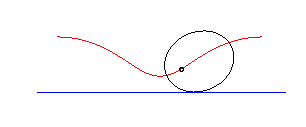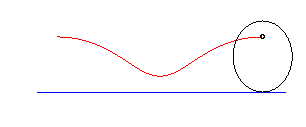roulette elliptique roulette hyperbolique

La roulette parabolique de Delaunay n'est autre que la chaînette.

Prenant Ox comme axe de roulement, la roulette de Delaunay est une courbe oscillant entre les droites et ; sur la droite y = b se trouvent dans le cas elliptique des points d'inflexion avec une pente égale à et des points à tangente verticale dans le cas hyperbolique. La période de y en fonction de x est donnée par l'intégrale elliptique l(2p) ; c'est la longueur de l'ellipse dans le cas elliptique.

L'ingénieux mécanisme articulé suivant permet de tracer les roulettes de Delaunay :

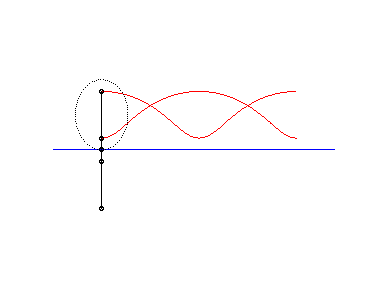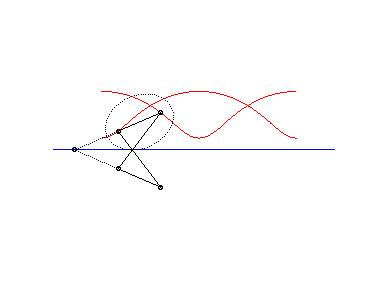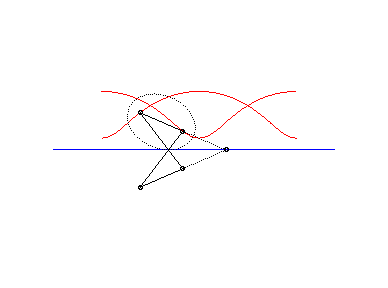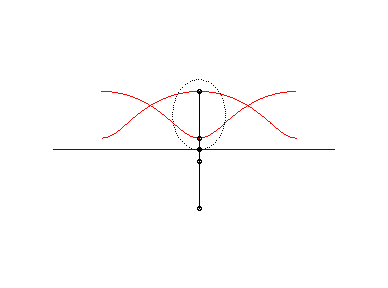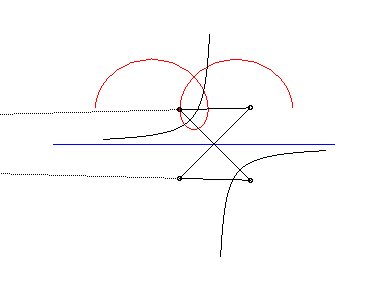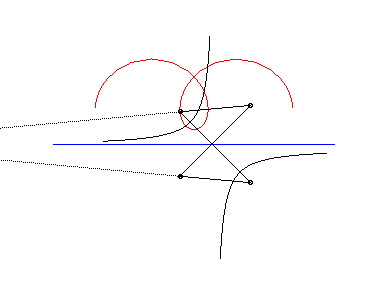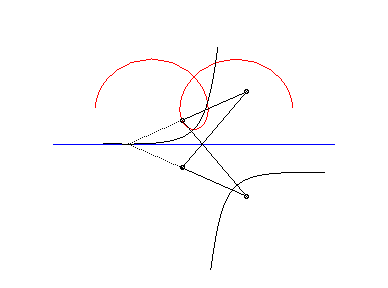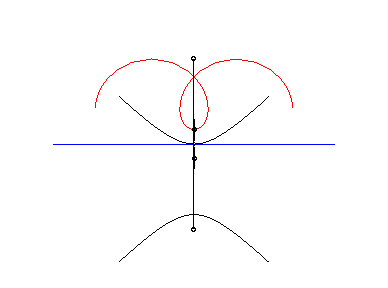On dispose d'un quadrangle articulé FF'GG' de cotés FF' = 2c et FG' = 2a ; les droites (FG') et (F'G) se coupent en P et les droites (FF') et (GG') se coupent en Q ; les points P et Q sont assujettis à se mouvoir sur la droite de roulement ; on met des roulettes sur les bras (FG') et (F'G) de sorte que leur déplacement soit constamment perpendiculaire à eux même ; F et F' sont alors les foyers de la conique, qui est tangente en P à la droite de roulement.

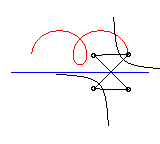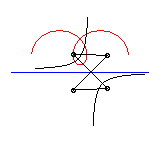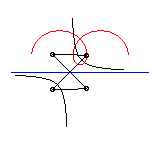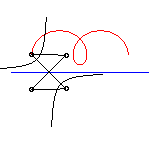Cette animation montre que dans le cas parabolique, la directrice de la parabole enveloppe la chaînette symétrique par rapport à l'axe de roulement ; cette directrice coupe la droite de roulement au même point que la tangente à la roulette au point correspondant.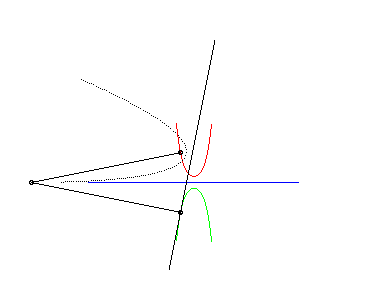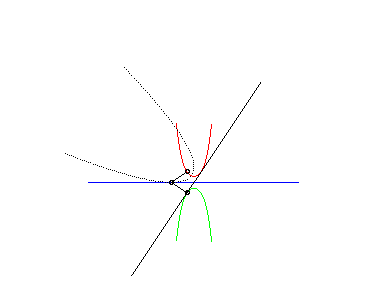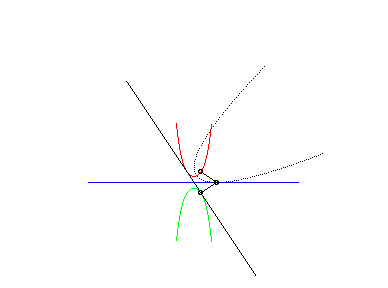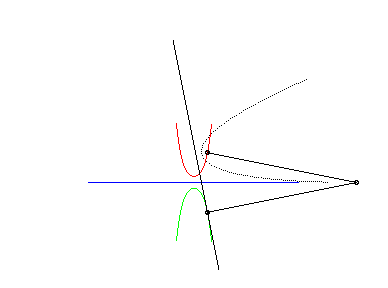

Ces courbes ont été considérées par Delaunay car elles ont la propriété d'être les seules courbes méridiennes des surfaces de révolution à courbure moyenne constante, lesquelles surfaces sont les surfaces de Delaunay.

Voir aussi les roulettes de Sturm, lieu du centre de la conique, aisni que la détermination de la route associée à une roue elliptique.

Lien : www.gang.umass.edu/gallery/cmc/cmcgallery0101.html

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres