Courbes étudiées par Lamé en 1818. Gabriel Lamé (1795-1870) : ingénieur et mathématicien français. Autres nom pour  > 2: super-ellipse, super-cercle (si a = b), en anglais : squircle (mot-valise formé à partir de square et circle).

 

Équation cartésienne :  ;  :  avec a, b > 0 ,  ;  Paramétrisation cartésienne de  : . Aire du domaine limité par  :  où  , soit  si .

Les courbes de Lamé  et  sont définies par leur équation cartésienne ci-dessus.
Pour  rationnel, la courbe , partie de  située dans le quadrant  est une portion de courbe algébrique  de degré pq ?  , d’équation  ? (lorsque p est pair,  et coïncident) ; même chose pour les courbes .

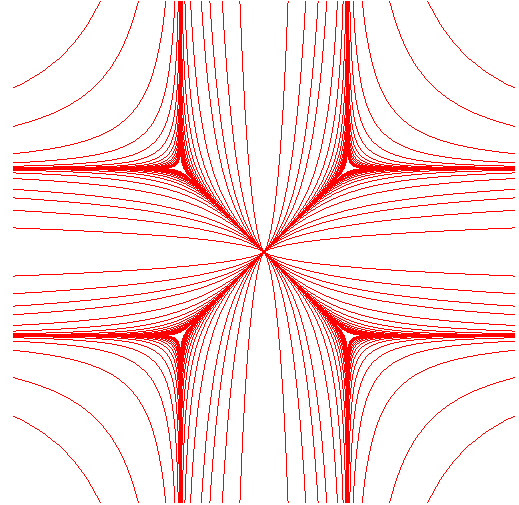
Exemples de courbes avec a = b :
 

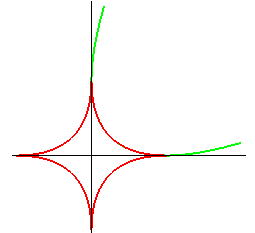
	courbe de Lamé	courbe algébrique associée	figure : la courbe de Lamé en rouge, la courbe algébrique associée en vert.
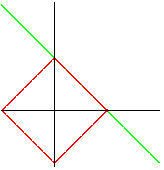
1	carré :	droite :
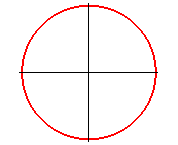
2	cercle :	idem
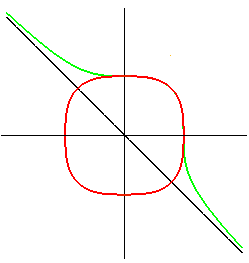
3		Cubique de Lamé :
	carré :
1/2	réunion de 4 arcs de parabole :	parabole :
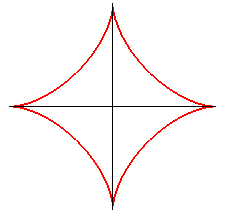
2/3	astroïde :	idem
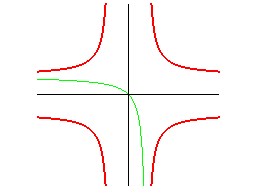
–1	réunion de 4 branches d’hyperboles équilatères :	hyperbole équilatère :
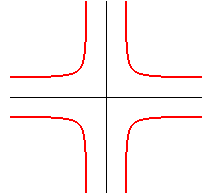
–2	cruciforme :	idem

 
 

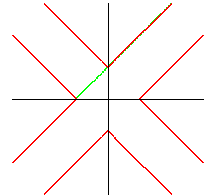
	courbe de Lamé	courbe algébrique associée	figure : la courbe de Lamé en rouge, la courbe algébrique associée en vert.
1	huit demi-droites :	droite :
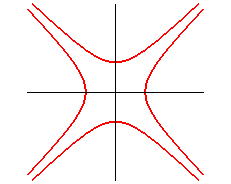
2		hyperbole équilatère :
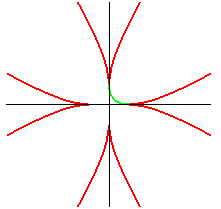
1/2	réunion de 8 arcs de parabole :	parabole :
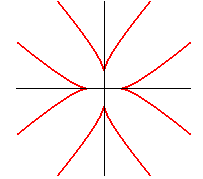
2/3	et sa symétrique par rapport à y = x, d'équation :	idem ; c'est la réunion de deux développées d'hyperbole.
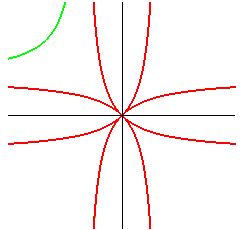
– 1	réunion de 8 branches d’hyperboles équilatères  :	hyperbole équilatère :
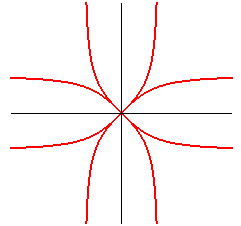
– 2		puntiforme :

Pour a = b =1 et a  = n entier naturel,  est la courbe de Fermat.

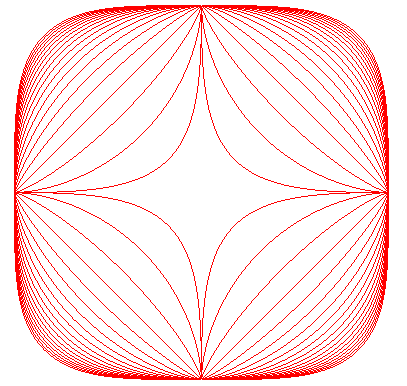
Voir aussi les surfaces de Lamé.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2016