ASTROÏDE
Astroid,
Astroide (od. Sternkurve)
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ASTROÏDE
Astroid,
Astroide (od. Sternkurve)

| Courbe étudiée par Ole
Rømer en 1674, Jean Bernoulli en 1691, Leibniz en 1715 et par
D'Alembert en 1748.
Nom donné par Littrow en 1838. "Astroïde" signifie "en forme d'astre" (même étymologie qu' astéroïde : qui ressemble à un astre !) Autres noms : H4 (hypocycloïde à quatre rebroussements), cubocycloïde. |
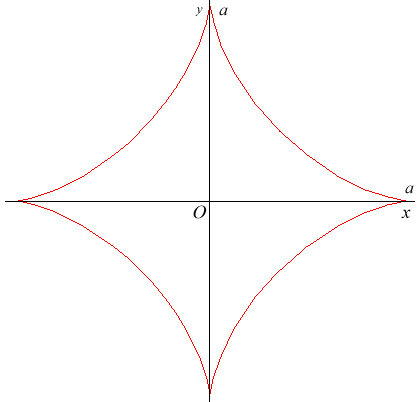 |
Paramétrisation cartésienne : Équation cartésienne : Sextique bicirculaire rationnelle. Paramétrisation complexe : Angle tangentiel cartésien : 1) Abscisse curviligne : 1) Rayon de courbure : 1) Équation intrinsèque 1 (cas 1)): Équation intrinsèque 2 (cas 1)): Équation podaire : Longueur : 6a. Aire : |
L’astroïde est une hypocycloïde
à quatre rebroussements (cercle de rayon a/4 (ou 3a/4)
roulant à l'intérieur d'un cercle (C) de rayon a).
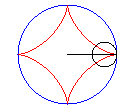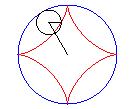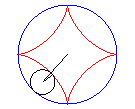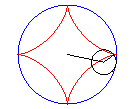  |

Animation de la double génération |
C’est donc l'enveloppe d'une corde (PQ) du cercle de centre O et de rayon a/2 (cercle inscrit dans l’astroïde), P et Q parcourant ce cercle dans des sens contraires, l’un ayant une vitesse triple de l’autre (génération de Cremona).

Ci-dessus, le point n est relié au point -3n modulo 30. |
 |
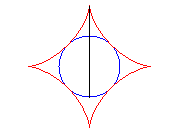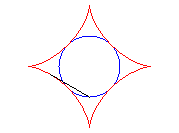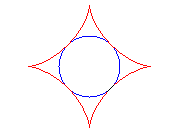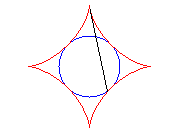 |
Et c’est aussi l’enveloppe d’un diamètre d'un cercle de rayon a/2 roulant à l'intérieur de (C).
Les extrémités de ce diamètre décrivent
deux segments perpendiculaires.
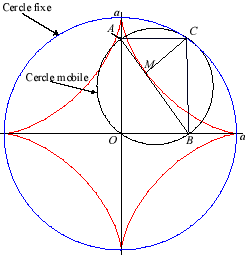
| L’astroïde est donc aussi l’enveloppe
d'un segment [AB] de longueur constante a dont les extrémités
se déplacent sur deux droites perpendiculaires. Le point de contact
M
est le projeté du sommet C du rectangle (OACB) sur
[AB] (et les points de la droite (AB) décrivent eux
une ellipse).
Le cas plus général où les droites ne sont pas perpendiculaires donne une tétracuspide. Voir aussi le berlingot
qui est la généralisation à l'espace de cette enveloppe.
|
 |
D'après cette propriété, le bord de la trace sur le marchepied d'une porte coulissante d'autobus à deux battants est un huitième d'astroïde, suivi d'un arc de cercle :
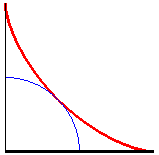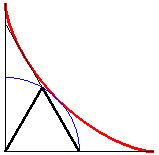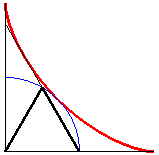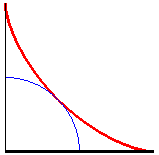
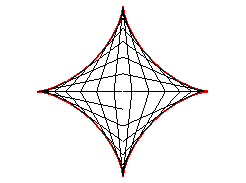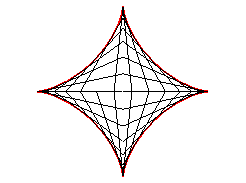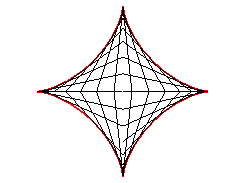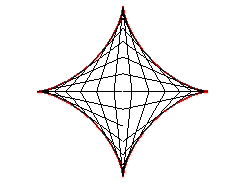
Remarque : la courbe déterminée par un tableau
de fils construit sur deux segments perpendiculaires n’est pas une
astroïde, mais une autre courbe de Lamé
qui est réunion de 4 arcs de paraboles
(la longueur du segment [AB] n’est dans ce cas pas constante).
L’astroïde est aussi l’enveloppe des ellipses ,
avec
(traces dans le plan des points du segment [AB] ci-dessus).
 |
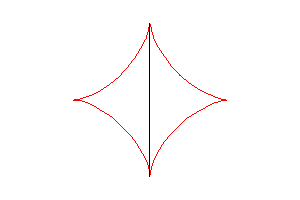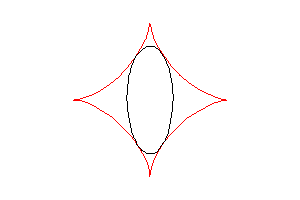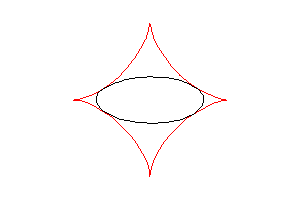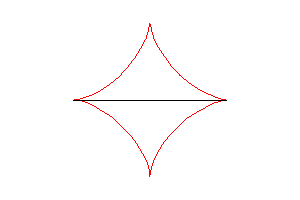 |
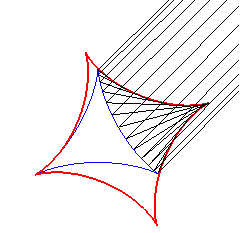
Elle est enfin la caustique
par réflexion d'une deltoïde,
avec des rayons incidents parallèles de direction quelconque (bien
comprendre comment une courbe à symétrie d'ordre 3 peut engendrer
une courbe à symétrie d'ordre 4 ! ).
 |
 |
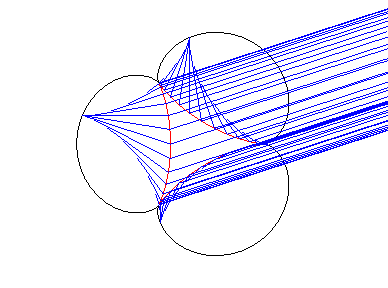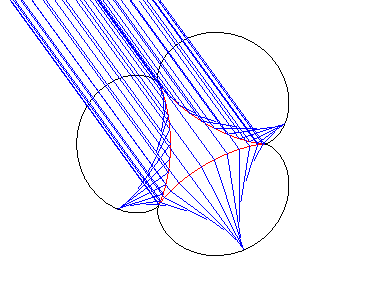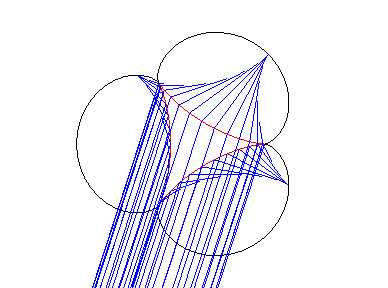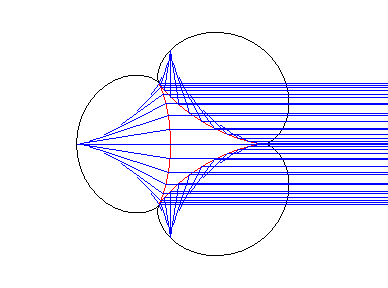
Lorsque les rayons incidents prennent toutes les directions possibles, les pointes de l'astroïde enveloppe décrivent une épicycloïde à 3 rebrousements. On a une propriété similaire avec la cubique de Tschirnhausen. |
| Comme pour toute courbe cycloïdale, la développée est une astroïde semblable (dans un rapport 2) : | 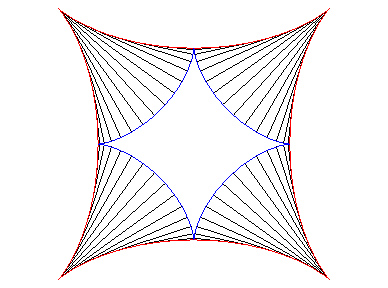 |
| L'une des développantes est donc une astroïde ; en voici deux autres (voir aussi la croix de Malte) : | 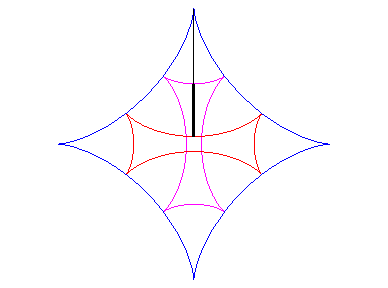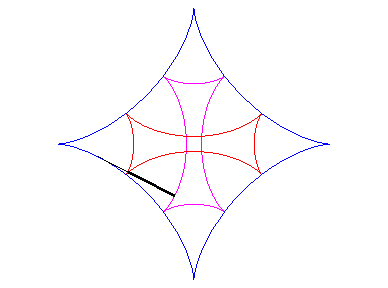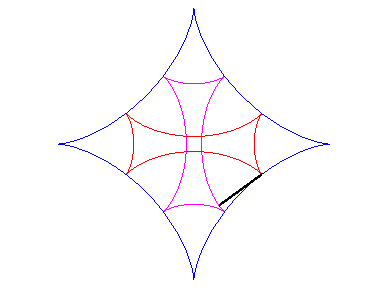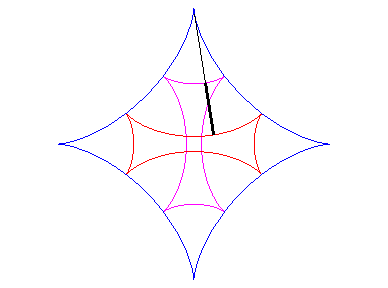 |
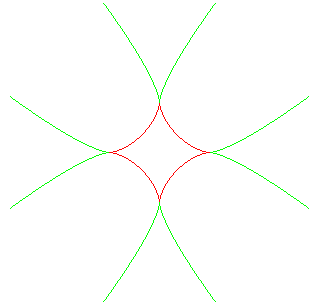
| La courbe d'équation cartésienne : On peut la définir simplement comme l'enveloppe des droites coupant Ox et Oy en P et Q tels que la somme ou la différence de OP² et OQ² est constante. |
 |
Les podaires d'astroïde sont les scarabées, en particulier, la podaire par rapport au centre est le trèfle à quatre feuilles, et la polaire réciproque est la cruciforme équilatère.
Voir aussi à tétracuspide.

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2006