CRUCIFORME
Crosscurve,
Kreuzkurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
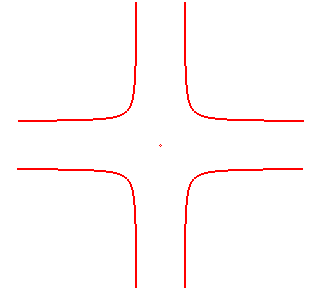
CRUCIFORME
Crosscurve,
Kreuzkurve

| Courbe étudiée par Terquem en 1847 et Pieter
Schoute en 1883.
En anglais aussi appelée : policeman on point-duty curve (courbe du flic au carrefour...) |
 |
Équation cartésienne : Paramétrisation cartésienne : Équation polaire pour a = b (cruciforme équilatère) : Quartique rationnelle. |
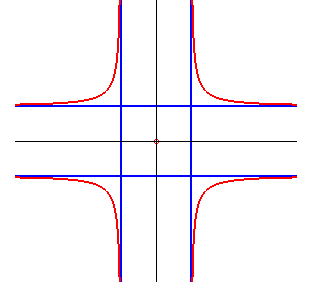
La cruciforme est l'image de l'ellipse par une inversion
biaxiale (d'axes ceux de l'ellipse), définie ici par : .
Les quatre asymptotes sont tangentes à l'ellipse de départ
en ses sommets.
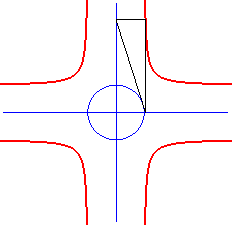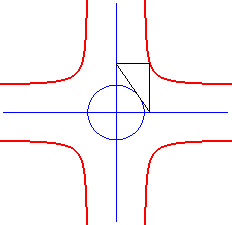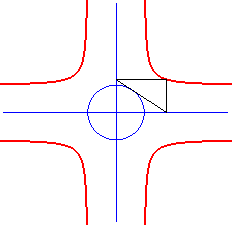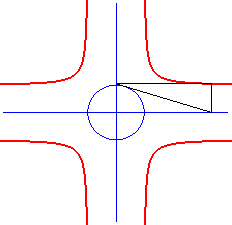
| On l'obtient géométriquement comme lieu
des points d'intersection des parallèles aux axes menées
des deux points d'intersection d'une tangente à l'ellipse avec les
axes.
La cruciforme est donc à l’ellipse ce que la puntiforme est à l’hyperbole. |
 |
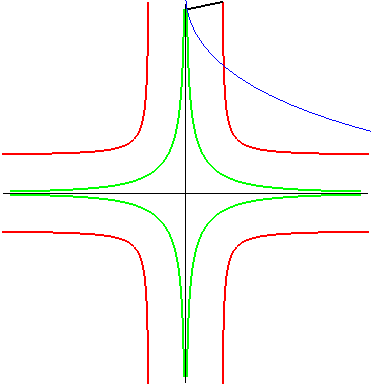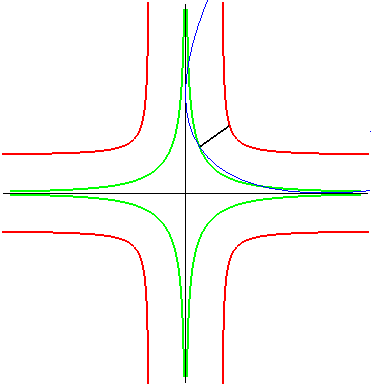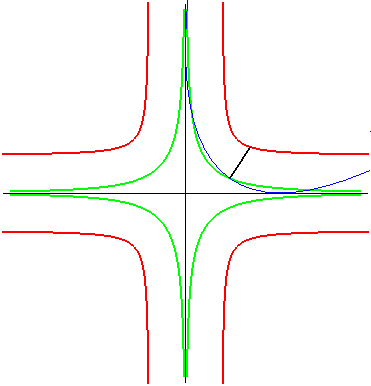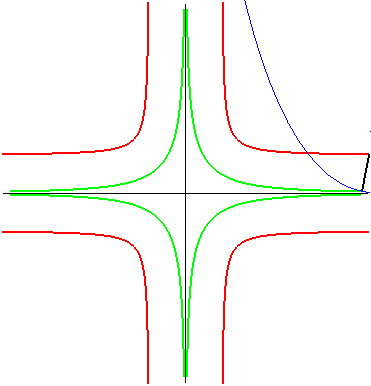
| La cruciforme équilatère est aussi le lieu
du foyer d'une parabole astreinte à rester tangente à deux
axes perpendiculaires ; c'est donc une glissette.
Pour une parabole de paramètre p, on obtient une cruciforme de paramètres a = b = p/2. Dans ce mouvement, le lieu du sommet de la parabole (en
vert ci-contre) est la courbe de paramétrisation : |
 |
| La cruciforme équilatère est la section plane d'un cône sinusoïdal. |  |
| Elle est aussi la projection sur xOy de l'intersection
du cône
de révolution Cette intersection a pour paramétrisation |
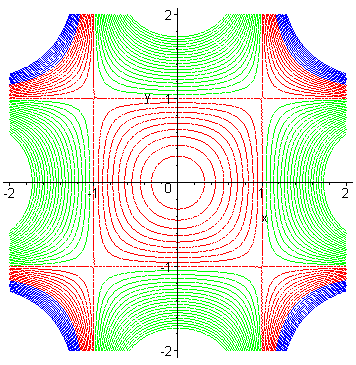
| Ci-contre, la famille des quartiques d'équation La cruciforme est obtenue pour k = 1 (limite entre les courbes bleues et rouges). Pour k > 0, ce sont les courbes de niveau du coussin de Bouligand. |
 |
L'inverse de la cruciforme équilatère par rapport à son centre est le quadrifolium, et sa polaire réciproque, l'astroïde.
Voir ici
l'orthoptique de la cruciforme.
Comparer avec l'inverse
biaxial de huit.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2020