La courbe du nageur est la trajectoire d'un nageur dans une rivière entraîné par un courant rectiligne de vitesse constante  et nageant à vitesse constante  vers un point fixe sur la rive (ici le point fixe est O et le sens du courant Oy) ; on peut aussi imaginer un bateau pointant vers une balise fixe.
 

Système différentiel donnant le mouvement du nageur :  en coordonnées cartésiennes, soit  en coordonnées polaires. Équation différentielle de la trajectoire :  en cartésiennes, ou  en polaires. Équation cartésienne de la courbe passant par A(a,b)  :  où  avec u = b/a. Équation polaire : . Courbe algébrique pour k rationnel. k  = 1 : parabole :  ; k = 2 : parabole divergente : .

On constate que le nageur atteint le point fixe ssi sa vitesse du courant est strictement inférieure à la sienne  ; lorsque la vitesse du courant augmente, le temps de traversée augmente, jusqu'au cas où ;  il atteint encore théoriquement la rive Oy, mais en aval de la cible, et en un temps infini ; sa trajectoire est alors un arc de parabole de foyer O. Lorsque la vitesse du courant est supérieure à la sienne, il se fait emporter par lui.

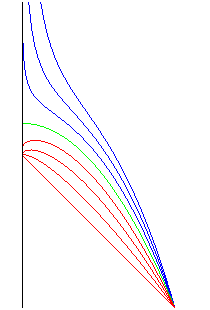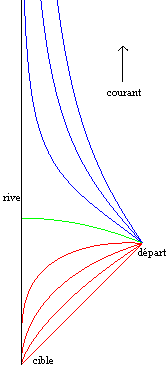
Ci-dessus, trois représentations des courbes, suivant que le point de départ du nageur est en aval, au droit, ou en amont de la cible. Pas de courant : cas = 0 : trajectoire rectiligne. En rouge : cas , soit  k > 1 : le nageur atteint encore sa cible après un détour. En vert : cas , soit k = 1: le nageur atteint encore la rive, mais pas la cible (la courbe est une parabole) En bleu : cas , soit k < 1 : le nageur s'approche de la rive sans jamais l'atteindre.

La trajectoire du nageur dans le plan mobile de la rivière est une courbe de poursuite (ce qui donne une méthode pour résoudre ce problème).

On peut généraliser ce problème en considérant deux plans (P) et (Q), le premier fixe et le deuxième mobile et les courbes dans (P) d'un point M de (Q) se dirigeant constamment en direction d'un point fixe O, à vitesse constante.

Par exemple, si le mouvement de (Q) est circulaire uniforme de centre O, la courbe de M dans (P) est une spirale d'Archimède.

Une autre généralisation est de considérer que l'axe du nageur (ou plutôt du bateau) fait constamment un angle a avec (OM) ; on obtient alors l'équation différentielle polaire : .
Pour k = 1, celle ci s'intègre en la parabole : .
Pour a = p/ 2, le résultat est remarquable, car le mouvement est le même que celui des planètes autour du soleil ; voir à conique.

On peut aussi considérer que le point vers lequel pointe le nageur se déplace lui aussi, ce qui donne une courbe de poursuite avec courant.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2004