Courbe étudiée par Huygens, Tschirnhausen en 1679, Jacques Bernoulli en 1692, Daniel Bernoulli en 1725 et Proctor qui a donné le nom en 1878. Du grec nephros "rein".

 
 

Paramétrisation complexe : . Paramétrisation cartésienne : . Équation cartésienne : . Sextique rationnelle. Équation polaire : . Abscisse curviligne : . Angle tangentiel cartésien : . Rayon de courbure : . Équation intrinsèque 1 : . Équation intrinsèque 2 : . Équation podaire : . Longueur : 12 a ; aire : 3pa2.

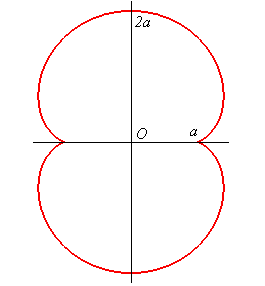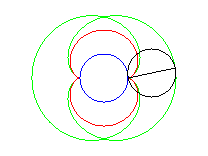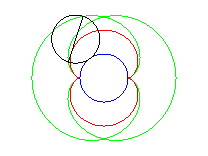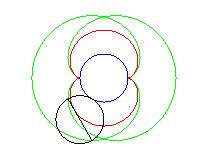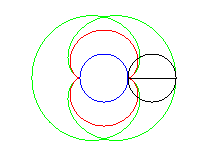
La néphroïde est une épicycloïde à deux rebroussements (cercle de rayon a/2 roulant à l'extérieur d'un cercle (C) de rayon a).

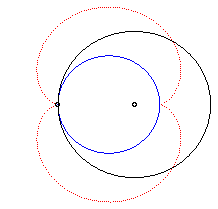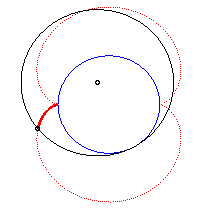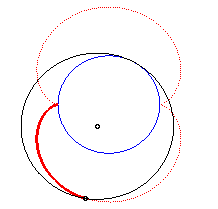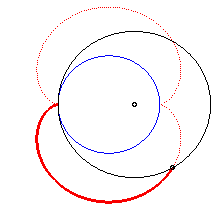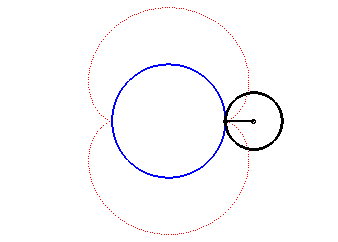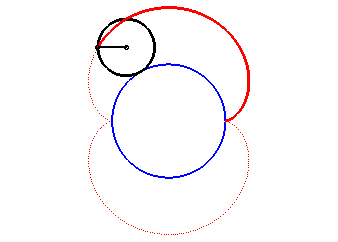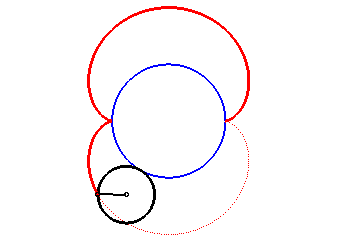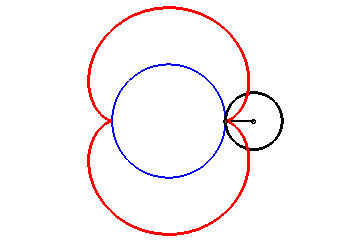
Animation de la double génération

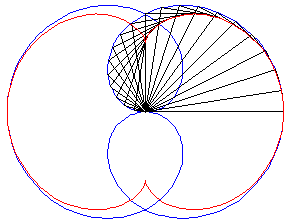
    - l'enveloppe d'un diamètre d'un cercle de rayon a roulant sans glisser sur et extérieurement à (C).

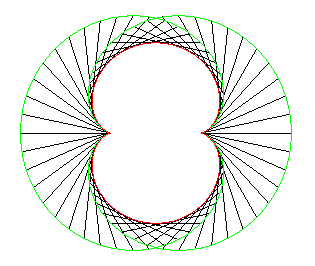
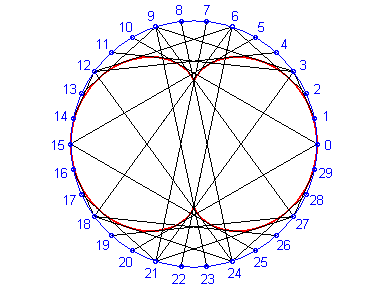
Ci-dessus, le point n est relié au point 3n modulo 30.

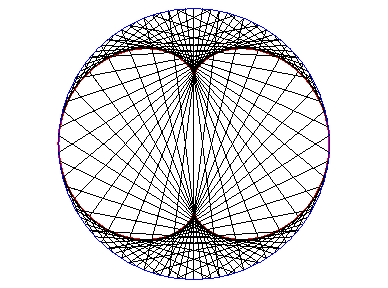La néphroïde est aussi :
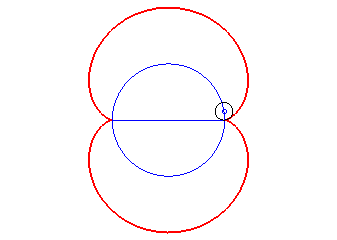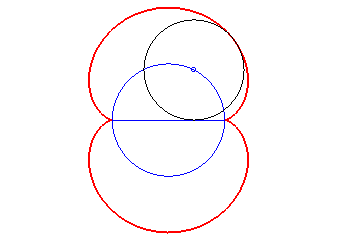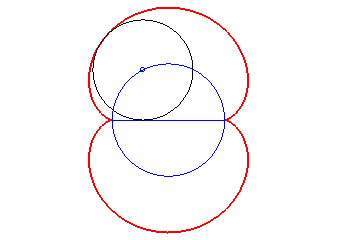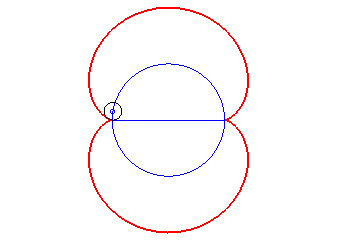
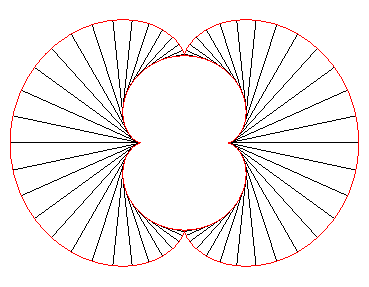
 - l’enveloppe des cercles centré sur un cercle (ici, (C)) et tangents à l’un de ses diamètres (ici Ox). La néphroîde est donc la la symétrique d'un diamètre d'un cercle par rapport à ce cercle.

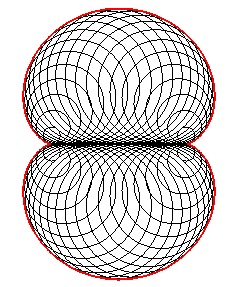
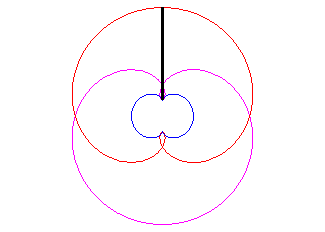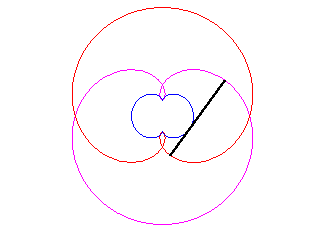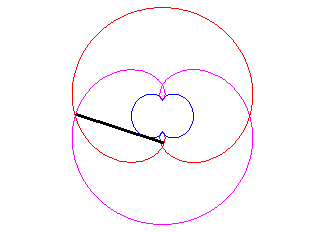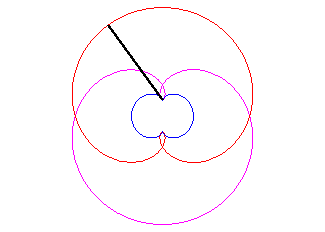
 - une caustique par réflexion de cercle (ici, (C)) avec source lumineuse à l’infini (ici, les rayons incidents parallèles à Ox).

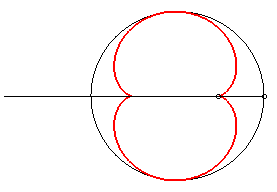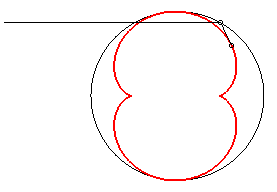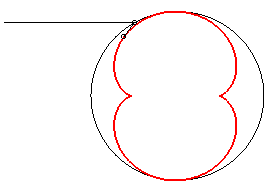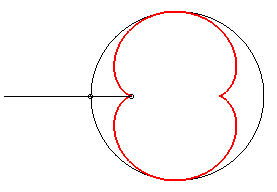
C'est cette propriété qui fait apparaître une demi-néphroïde dans votre tasse de café, ou ici dans un plat émaillé :

Voir aussi à cardioïde.

 - une caustique par réflexion de cardioïde, la source lumineuse se trouvant au point de rebroussement de la cardioïde. C'est donc aussi la développée de la sextique de Cayley, qui est son orthotomique (ou sa podaire).

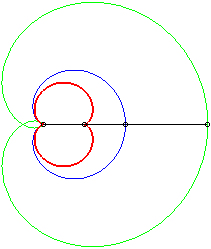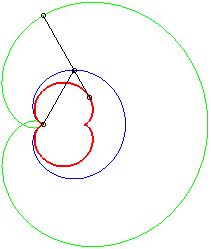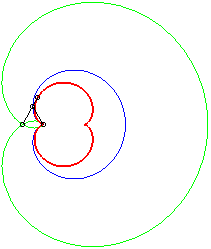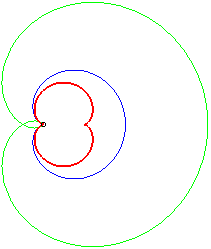
    - une antipodaire de la rosace  r = 2a sin q/2 :

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2012