Courbe étudiée par Hipparque au IIème siècle avant J.C., Dürer en 1525, RØmer en 1674 et Daniel Bernoulli en 1725. Préfixe provenant du grec epi  "sur".

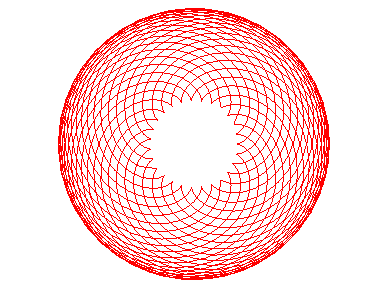
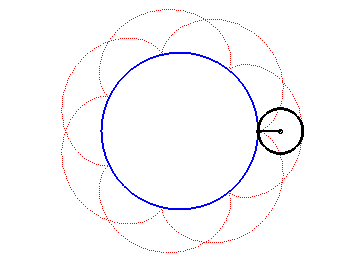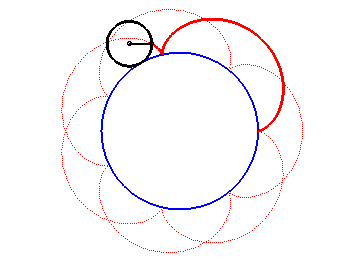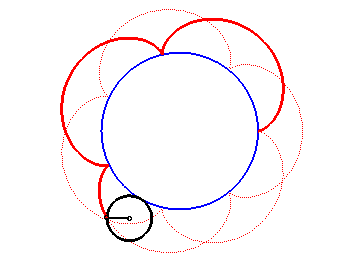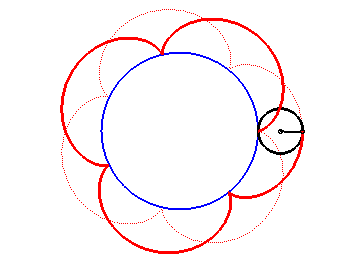
Les épicycloïdes sont les courbes décrites par un point d'un cercle (C) roulant sans glisser sur un cercle de base (C₀), les disques ouverts de frontières (C) et (C₀) étant disjoints ; ce sont donc des cas particuliers d'épitrochoïdes.

Paramétrisation complexe :  ou  où a est le rayon du cercle de base et  celui du cercle roulant. Paramétrisation cartésienne : . Rayon vecteur :  ; angle polaire donné par . Abscisse curviligne donnée par (d'où l'équation différentielle )   Deux expressions intéressantes pour l'abscisse curviligne ; origine au début d’une arche (cas 2) ou en son milieu (cas 1) : 1)  2) . Angle tangentiel cartésien : . Rayon de courbure : . Équation intrinsèque 1 : . ( est l’équation d’une épicycloïde si et seulement si d > c, avec ) Équation intrinsèque 2 :. ( est l'équation d'une épicycloïde si et seulement si |B| < 1). Équation podaire : .  Equation de la tangente en M(t) : . Longueur d’une arche : . Aire de la surface située entre l'arche et les deux tangentes à ses extrémités : .

Les épicycloïdes sont des courbes formées d'arcs isométriques (les arches) se rejoignant en des points de rebroussements (obtenus pour ) en nombre égal au numérateur du nombre q si q est rationnel et en nombre infini sinon.
Lorsque q est rationnel, , la courbe est algébrique rationnelle (prendre comme  paramètre ).
Elle ressemble à un polygone régulier, croisé si m ³ 2, à n sommets joints de m en m par des courbes situées à l’extérieur du cercle (C₀).

Lorsque l'on parle d'épicycloïde simple à n rebroussements (E_n), on considère le cas q = n, c'est-à-dire celui où il n'y a pas de croisement.
Informations dans ce cas :
 

Longueur totale : , qui tend vers 8a, et non vers  comme on pourrait le penser. Aire totale englobée : , qui tend bien vers . Lorsque le cercle roulant revient à son point de départ, il tourne n + 1 fois autour du cercle fixe.

 

q = 1 : cardioïde	q  = 2 : néphroïde.	q = 3	q = 4	q = 5
q = 1/2 : double cardioïde	q = 3/2	q = 5/2	q = 7/2	q = 9/2
q  = 1/3	q = 2/3	q = 4/3	q = 5/3	q = 7/3
q = 1/4	q = 3/4	q = 5/4	q = 7/4	q = 9/4
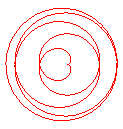
q = 1/5	q = 2/5	q = 3/5	q = 4/5	q = 6/5

 

L'épicycloïde est aussi la courbe décrite par un point d'un cercle de rayon  () roulant sans glisser sur (C0) en le contenant (ceci constitue la double génération de l'épicycloïde : voir à péricycloïde).

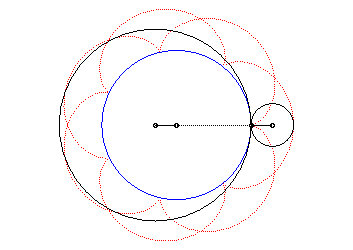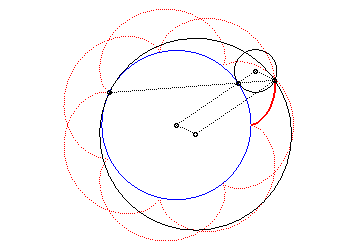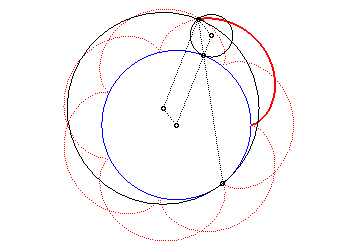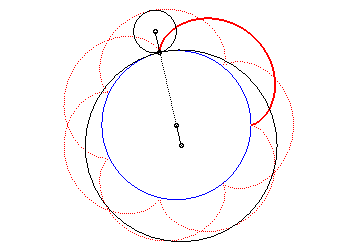L’épicycloïde est l'enveloppe d'un diamètre d'un cercle de rayon double de celui de (C) roulant sans glisser sur et extérieurement à (C₀).

C'est aussi l'enveloppe d'une corde (PQ) du cercle de rayon a + 2b (cercle des sommets de l'épicycloïde), P et Q parcourant ce cercle dans le même sens et avec des vitesses constantes dans le rapport q + 1 (ceci constitue la génération dite de Cremona). Voir cette vidéo de Michael Launay, pour une présentation originale.
Si l'on considère que les planètes ont des mouvements circulaires uniformes dans un plan autour du soleil, la droite qui joint les deux planètes enveloppe donc une épicycloïde (voir par exemple, cette vidéo).
C’est enfin l’antipodaire par rapport à O de la rosace : .

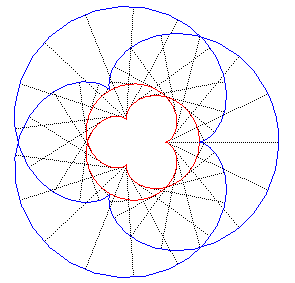
Sa développée est sa propre image par la similitude directe de centre O, de rapport , et d’angle .

L'une de ses développantes est donc une épicycloïde semblable ; lorsque le numérateur de q est impair les autres développantes sont des courbes auto-parallèles .
 

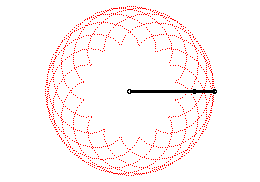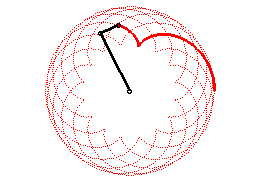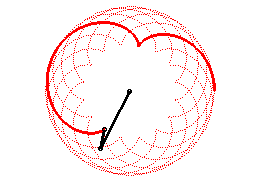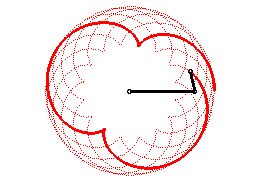
On peut aussi définir les épicycloïdes comme les trajectoires d’un mouvement somme de deux mouvements circulaires uniformes de même vitesse et de mêmes sens (de paramétrisation complexe :  avec ).
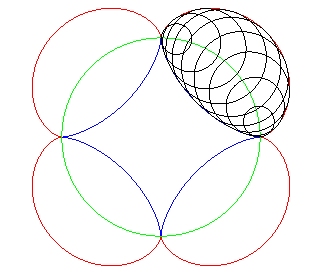
L'épicycloïde est la symétrique de l'hypocycloïde tracée avec le même cercle. Par exemple, ci-contre, l'épicycloïde à 4 rebroussements est la symétrique de l'astroïde.

Les épicycloïdes sont des cas particuliers de courbe cycloïdale, avec les hypocycloïdes et la cycloïde.

Ce sont aussi des projections d'hélices sphériques.

L'équation différentielle  montre, via l'équation d'Euler-Lagrange, que, de même que la cycloïde, l'épicycloïde est une courbe brachistochrone : c'est la courbe plane qui minimise le temps de parcours d'un mobile se déplaçant librement le long de cette courbe, cette courbe tournant à vitesse constante autour d'un centre fixe O, dans le cas où le mobile a une vitesse nulle lorsqu'il est à distance a de O (lorsque a est nul la brachistochrone est alors la spirale logarithmique).

On retrouve les épicycloïdes comme frontières des composantes principles des ensembles de Mandelbrot associés à .

Voir aussi sur cette page les roulettes d'ellipses roulant sur une ellipse.

Voir aussi en 3D les épicycloïdes  sphériques.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Jacques MANDONNET 2016